题目内容
5.在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,则λ+μ的最大值为( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
分析 如图:以A为原点,以AB,AD所在的直线为x,y轴建立如图所示的坐标系,先求出圆的标准方程,再设点P的坐标为($\frac{2\sqrt{5}}{5}$cosθ+1,$\frac{2\sqrt{5}}{5}$sinθ+2),根据$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,求出λ,μ,根据三角函数的性质即可求出最值.
解答 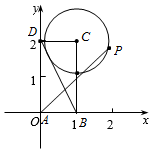 解:如图:以A为原点,以AB,AD所在的直线为x,y轴建立如图所示的坐标系,
解:如图:以A为原点,以AB,AD所在的直线为x,y轴建立如图所示的坐标系,
则A(0,0),B(1,0),D(0,2),C(1,2),
∵动点P在以点C为圆心且与BD相切的圆上,
设圆的半径为r,
∵BC=2,CD=1,
∴BD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$
∴$\frac{1}{2}$BC•CD=$\frac{1}{2}$BD•r,
∴r=$\frac{2}{\sqrt{5}}$,
∴圆的方程为(x-1)2+(y-2)2=$\frac{4}{5}$,
设点P的坐标为($\frac{2\sqrt{5}}{5}$cosθ+1,$\frac{2\sqrt{5}}{5}$sinθ+2),
∵$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,
∴($\frac{2\sqrt{5}}{5}$cosθ+1,$\frac{2\sqrt{5}}{5}$sinθ+2)=λ(1,0)+μ(0,2)=(λ,2μ),
∴$\frac{2\sqrt{5}}{5}$cosθ+1=λ,$\frac{2\sqrt{5}}{5}$sinθ+2=2μ,
∴λ+μ=$\frac{2\sqrt{5}}{5}$cosθ+$\frac{\sqrt{5}}{5}$sinθ+2=sin(θ+φ)+2,其中tanφ=2,
∵-1≤sin(θ+φ)≤1,
∴1≤λ+μ≤3,
故λ+μ的最大值为3,
故选:A
点评 本题考查了向量的坐标运算以及圆的方程和三角函数的性质,关键是设点P的坐标,考查了学生的运算能力和转化能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案 若执行右侧的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )
若执行右侧的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )| A. | x>3 | B. | x>4 | C. | x≤4 | D. | x≤5 |
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |