Question

4．已知a、b∈R，ab≠0，函数f（x）=$\frac{ax}{x+b}$图象的对称中心坐标为（-1，1）．
（1）求a、b的值；
（2）若P（x，y）是函数y=f（x）图象上的动点，且x＜-1，试求OP（O为坐标原点）的最小值，并求此时点P的坐标．

Answer 1

分析 （1）根据函数的图象和性质，以及对称中心的定义，即可求出a，b的值，
（2）画出函数的图象，当过点P的切线与OP垂直时，OP（O为坐标原点）有最小值，利用导数的几何意义即可求出点P的坐标，问题得以解决．

解答 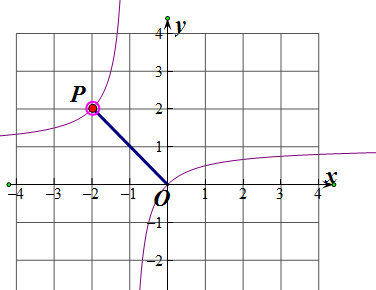解：（1）∵函数f（x）=$\frac{ax}{x+b}$=$\frac{a（x+b）-ab}{x+b}$=-$\frac{ab}{x+b}$+a图象的对称中心坐标为（-1，1），
∴a=1，b=1
（2）由（1）知f（x）=$\frac{x}{x+1}$，P（x，y）是函数y=f（x）图象上的动点，且x＜-1，
图象如图所示，
当过点P的切线与OP垂直时，OP（O为坐标原点）有最小值，
∵f′（x）=$\frac{1}{（x+1）^{2}}$，
∴切线的斜率k=f′（x）=$\frac{1}{（x+1）^{2}}$，
∵k_OP=$\frac{y}{x}$=$\frac{1}{x+1}$，
∴k•k_OP=-1，
∴$\frac{1}{（x+1）^{2}}$•$\frac{1}{x+1}$=-1，
解得x=-2，
∴y=$\frac{-2}{-2+1}$=2，
∴点P的坐标为（-2，2），
∴OP（O为坐标原点）的最小值为$\sqrt{（-2）^{2}+{2}^{2}}$=2$\sqrt{2}$

点评 本题考查了函数的对称中心的性质，以及导数的几何意义，关键是画出图象得到当过点P的切线与OP垂直时，OP（O为坐标原点）有最小值，属于中档题．