题目内容
12.已知向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(1,2),$\overrightarrow{c}$=(-1,3),若($\overrightarrow{a}$+2$\overrightarrow{b}$)∥$\overrightarrow{c}$,则实数x的值为( )| A. | -$\frac{11}{3}$ | B. | -17 | C. | 12 | D. | 13 |
分析 利用已知条件求出$\overrightarrow{a}$+2$\overrightarrow{b}$,然后利用向量的平行列出方程求解x即可、
解答 解:向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(1,2),$\overrightarrow{c}$=(-1,3),
$\overrightarrow{a}$+2$\overrightarrow{b}$=(x+2,5),
∵($\overrightarrow{a}$+2$\overrightarrow{b}$)∥$\overrightarrow{c}$,
∴3x+6=-5,
解得x=$-\frac{11}{3}$.
故选:A.
点评 本题考查向量的共线以及坐标运算,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知三棱锥P-ABC的四个顶点都在球O的球面上,若PA=AB=2,AC=1,∠BAC=120°,且PA⊥平面ABC,则球O的表面积为( )
| A. | $\frac{40π}{3}$ | B. | $\frac{50π}{3}$ | C. | 12π | D. | 15π |
16.已知程序框图如图所示,则该程序框图的功能是( )


| A. | 求1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$的值 | B. | 求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$…+$\frac{1}{20}$的值 | ||
| C. | 求1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$的值 | D. | 求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$…+$\frac{1}{22}$的值 |
3.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点到一条渐近线的距离为a,则双曲线的离心率等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
20.阅读如图的程序框图,若输出的y=$\frac{1}{2}$,则输入的x的值可能为( )


| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
20.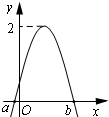 如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
 如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
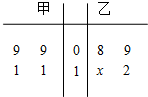 如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.