题目内容
19.函数 y=$\frac{1}{2}{x^2}-2$在点(1,-$\frac{3}{2}$)处的切线方程为2x-2y-5=0.分析 求出函数的导数,得到切线的斜率,然后求解切线方程.
解答 解:函数 y=$\frac{1}{2}{x^2}-2$,可得y′=x,函数 y=$\frac{1}{2}{x^2}-2$在点(1,-$\frac{3}{2}$)处的切线的斜率为:1.
所求切线方程为:y+$\frac{3}{2}$=x-1.即2x-2y-5=0.
故答案为:2x-2y-5=0.
点评 本题考查函数的导数的应用,切线方程的求法,考查计算能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
15.经过两点(-1,2),(-3,-2)的直线的方程是( )
| A. | x-2y+5=0 | B. | x-2y-5=0 | C. | 2x-y-4=0 | D. | 2x-y+4=0 |
8.设P={x|x<1},Q={x|x2<1},则( )
| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |
9.已知三棱锥S-ABC,其三视图中的正(主)视图和侧(左)视图如图所示,则该三棱锥的体积为( )
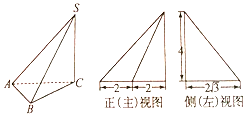

| A. | $\frac{{8\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $16\sqrt{3}$ |