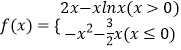题目内容
【题目】已知![]() 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且![]() ,若任意的
,若任意的![]() ,当
,当![]() 时,总有
时,总有![]() .
.
(1)判断函数![]() 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式:![]() ;
;
(3)若![]() 对所有的
对所有的![]() 恒成立,其中
恒成立,其中![]() (
(![]() 是常数),求实数
是常数),求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .(3)见解析.
.(3)见解析.
【解析】
(1)任取x1、x2两数使x1、x2∈[-1,1],且x1<x2,进而根据函数为奇函数推知f(x1)-f(x2)=f(x1)+f(-x2),让f(x1)+f(-x2)除以x1-x2再乘以x1-x2配出![]() 的形式,然后进而判定。
的形式,然后进而判定。
(2)根据函数f(x)在[-1,1]上是增函数知x满足的不等式组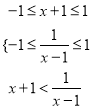 ,进而可解得x的范围
,进而可解得x的范围
(3)由(1)知![]() 最大值为
最大值为![]() ,所以要使
,所以要使![]() 对所有的
对所有的![]() 恒成立,只需
恒成立,只需![]() 成立,即
成立,即![]() 成立.对p讨论得到。
成立.对p讨论得到。
(1)![]() 在
在![]() 上是增函数,证明如下:
上是增函数,证明如下:
任取![]() ,且
,且![]() ,则
,则![]() ,于是有
,于是有![]() ,
,
而![]() ,故
,故![]() ,故
,故![]() 在
在![]() 上是增函数
上是增函数
(2)由![]() 在
在![]() 上是增函数知:
上是增函数知:
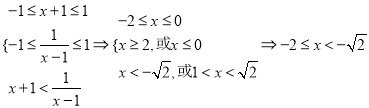 ,
,
故不等式的解集为![]() .
.
(3)由(1)知![]() 最大值为
最大值为![]() ,所以要使
,所以要使![]() 对所有的
对所有的![]() 恒成立,
恒成立,
只需![]() 成立,即
成立,即![]() 成立.
成立.
① 当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ;
;
②当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ;
;
③当![]() 时,
时,![]() 的取值范围为R.
的取值范围为R.

练习册系列答案
相关题目