题目内容
若非零函数 对任意实数
对任意实数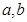 均有
均有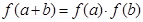 ,且当
,且当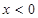 时,
时,  ;
;
(1)求证: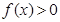 (2)求证:
(2)求证: 为减函数
为减函数
(3)当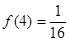 时,解不等式
时,解不等式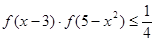
(1)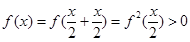 ;
;
(2)见解析;(3)不等式的解集为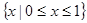 。
。
解析试题分析:(1)利用已知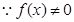
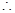
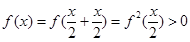 ,可得结论。
,可得结论。
(2)根据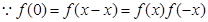 =1,得到f(x)与f(-x)的关系式,进而求解得到。
=1,得到f(x)与f(-x)的关系式,进而求解得到。
(3)由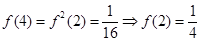 原不等式转化为
原不等式转化为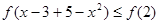 进而结合单调性得到。
进而结合单调性得到。
解:(1)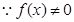
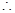
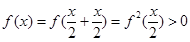 ------------3分
------------3分
(2)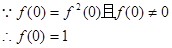 -------------5分
-------------5分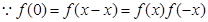
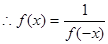 -------------8分
-------------8分
设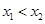 则
则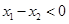
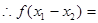
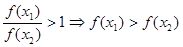 ,
, 为减函数
为减函数
-------10分
(3)由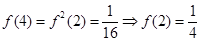 原不等式转化为
原不等式转化为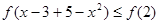 ,结合(2)得:
,结合(2)得: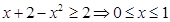
故不等式的解集为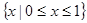 ------------------13分
------------------13分
考点:本题主要考查了函数的性质以及不等式的求解的运用。
点评:解决该试题的关键是抽象函数的赋值法思想的运用,判定单调性和f(x)与f(-x)的关系式的运用。

练习册系列答案
相关题目
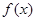 是定义在
是定义在 上的奇函数,当
上的奇函数,当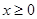 时,
时,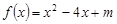 。
。
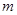 及
及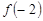 的值;
的值;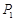 (元)和
(元)和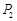 (元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.
(元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.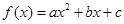 的零点是-1和3,当
的零点是-1和3,当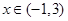 时,
时,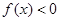 ,且
,且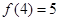 。(1)求该二次函数的解析式;(2)求函数
。(1)求该二次函数的解析式;(2)求函数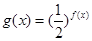 的最大值。
的最大值。 米.
米.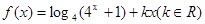 是偶函数
是偶函数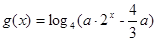 ,若函数f(x)与g(x)的图像有且只有一个公共点,求实数a的取值范围。
,若函数f(x)与g(x)的图像有且只有一个公共点,求实数a的取值范围。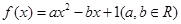 ,
,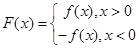
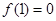 且对任意实数
且对任意实数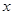 均有
均有 ,求
,求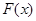 的解析式;
的解析式;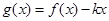 在区间
在区间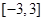 是单调函数,求实数
是单调函数,求实数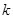 的取值范围;
的取值范围;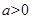 且
且 为偶函数,如果
为偶函数,如果 ,求证:
,求证: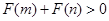 .
. -4÷
-4÷ ;
; .
. ,
, ,其中
,其中 是自然常数).
是自然常数). 的单调性和极小值;
的单调性和极小值; 在
在 上单调递增;
上单调递增; .
.