题目内容
(本题满分13分)已知函数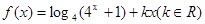 是偶函数
是偶函数
(1)求k的值;
(2)设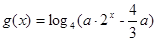 ,若函数f(x)与g(x)的图像有且只有一个公共点,求实数a的取值范围。
,若函数f(x)与g(x)的图像有且只有一个公共点,求实数a的取值范围。
(1) ;(2)
;(2)
解析试题分析:(1)
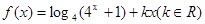 是偶函数
是偶函数 恒成立,即:(2k+1)x=0恒成立,所以
恒成立,即:(2k+1)x=0恒成立,所以
(2)由已知得 只有一个解
只有一个解
方程等价于 换元法得到
换元法得到
设
进而分类讨论的都参数的值。
(1)
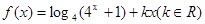 是偶函数
是偶函数 恒成立,即:(2k+1)x=0恒成立,所以
恒成立,即:(2k+1)x=0恒成立,所以
(2)由已知得 只有一个解
只有一个解
方程等价于
设


由h(0)=-1<0知方程有一解; 由h(0)<0知,要方程在(0,+
由h(0)<0知,要方程在(0,+ )只有一解,要满足:
)只有一解,要满足:
综上可知:
考点:本题主要考查了函数的奇偶性与方程解的问题的综合运用。
点评:解决该试题的关键是利用奇偶性得到参数k的值,然后借助于方程有一解,那么说明等价于 ,
,
构造函数 来解决。
来解决。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 为定义在
为定义在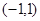 上的奇函数,当
上的奇函数,当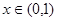 时,
时,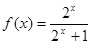
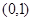 是增函数(2)求
是增函数(2)求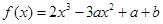 (其中a,b为实常数)。
(其中a,b为实常数)。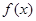 的单调区间:
的单调区间: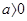 时,函数
时,函数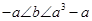 :
: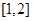 上是减函数,设关于x的方程
上是减函数,设关于x的方程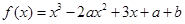 的两个非零实数根为
的两个非零实数根为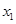 ,
,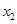 。试问是否存在实数m,使得
。试问是否存在实数m,使得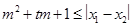 对任意满足条件的a及t
对任意满足条件的a及t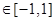 恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。 。
。 成立的
成立的 的取值范围;
的取值范围; 的最小值。
的最小值。 对任意实数
对任意实数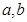 均有
均有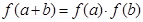 ,且当
,且当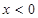 时,
时,  ;
;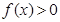 (2)求证:
(2)求证: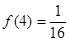 时,解不等式
时,解不等式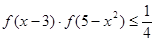
 )
)