题目内容
4.已知函数$f(x)=1+x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+…-\frac{{{x^{2016}}}}{2016}$(其中x>0),g(x)=lnx+x-3,设函数F(x)=f(x-1)g(x+1),且函数F(x)的零点都在区间[a,b](a<b,a∈Z,b∈Z)内,则b-a的最小值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 令F(x)=0,即为f(x-1)=0或g(x+1)=0,分别判断函数g(x),f(x)的单调性,判断g(1),g(2);f(-1),f(0)的符号,结合零点存在定理,即可得到a,b,进而得到最小值.
解答 解:函数F(x)=f(x-1)g(x+1),
可得F(x)=0,即为f(x-1)=0或g(x+1)=0,
由g(x+1)=ln(x+1)+x-2,
可得y=g(x+1)在(0,+∞)递增,
且g(1)=ln1-2=-2<0,g(2)=ln3>0,
可得g(x+1)的零点介于(0,1);
由函数$f(x)=1+x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+…-\frac{{{x^{2016}}}}{2016}$的导数为
f′(x)=1-x+x2-x3+…-x2015
=$\frac{1-(-x)^{2016}}{1+x}$>0,可得f(x)在x>0递增,
且y=f(x-1)递增,由f(-1)=1-1-$\frac{1}{2}$-$\frac{1}{3}$-…-$\frac{1}{2016}$<0,
f(0)=1>0,f(1)>0,f(2)>0,
介于y=f(x-1)的零点介于(-1,0),
则F(x)的零点都在区间[-1,1]内,
则b-a的最小值为2.
故选:A.
点评 本题考查函数的零点的判断,注意运用转化思想和函数的零点存在定理,考查判断和运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列函数中x=0是极值点的函数是( )
| A. | f(x)=-x3 | B. | f(x)=x2 | C. | f(x)=sinx-x | D. | f(x)=$\frac{1}{x}$ |
16.已知集合A={y|y=x${\;}^{\frac{2}{3}}$,x≥1},B={y|y=($\frac{1}{2}$)x,x≥-1},则A∩B=( )
| A. | {y|1≤y≤2} | B. | {y|y≥2} | C. | {y|$\frac{1}{2}$≤y≤1} | D. | {y|y≥1} |
14.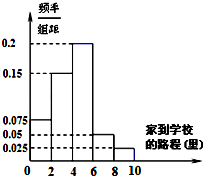 某高中地处市区,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
某高中地处市区,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
①若把家到学校的距离分为五个区间:[0,2)、[2,4)、[4,6)、[6,8)、[8,10),午休的走读生的分布情况如频率分布直方图所示;
②走读生是否午休与下午开始上课的时间有着密切的关系. 5次调查结果的统计表如表:
(1)若随机地调查一位午休的走读生,估计家到学校的路程(单位:里)在[2,6)的概率是多少?
(2)如果把下午开始上课时间2:10作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试列出x与y的统计表,并根据表中的数据求平均每天午休人数$\widehat{y}$与上课时间x之间的线性回归方程$\widehat{y}$=bx+a;
(3)预测当下午上课时间推迟到3:00时,家距学校的路程在6里路以上的走读生中约有多少人午休?
(注:线性回归直线方程系数公式b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.)
 某高中地处市区,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
某高中地处市区,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:①若把家到学校的距离分为五个区间:[0,2)、[2,4)、[4,6)、[6,8)、[8,10),午休的走读生的分布情况如频率分布直方图所示;
②走读生是否午休与下午开始上课的时间有着密切的关系. 5次调查结果的统计表如表:
| 下午开始 上课时间 | 2:10 | 2:20 | 2:30 | 2:40 | 2:50 |
| 平均每天 午休人数 | 250 | 350 | 500 | 650 | 750 |
(2)如果把下午开始上课时间2:10作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试列出x与y的统计表,并根据表中的数据求平均每天午休人数$\widehat{y}$与上课时间x之间的线性回归方程$\widehat{y}$=bx+a;
(3)预测当下午上课时间推迟到3:00时,家距学校的路程在6里路以上的走读生中约有多少人午休?
(注:线性回归直线方程系数公式b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.)