题目内容
阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------① ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明: ;
;
(Ⅱ)若 的三个内角
的三个内角 满足
满足 ,试判断
,试判断 的形状.
的形状.
(1)根据两角和差的余弦公式可以得到结论,
(2) 为直角三角形
为直角三角形
解析试题分析:解:解法一:(Ⅰ)因为 , ①
, ① , ② 2分
, ② 2分
①-② 得 . ③ 3分
. ③ 3分
令 有
有 ,
,
代入③得 . 6分
. 6分
(Ⅱ)由二倍角公式, 可化为
可化为 , 8分
, 8分
即 . 9分
. 9分
设 的三个内角A,B,C所对的边分别为
的三个内角A,B,C所对的边分别为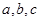 ,
,
由正弦定理可得 11分
11分
根据勾股定理的逆定理知 为直角三角形. 12分
为直角三角形. 12分
解法二:(Ⅰ)同解法一.
(Ⅱ)利用(Ⅰ)中的结论和二倍角公式,  可化为
可化为 , 8分
, 8分
因为A,B,C为 的内角,所以
的内角,所以 ,
,
所以 .
.
又因为 ,所以
,所以 ,
,
所以 .
.
从而 . 10分
. 10分
又因为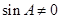 ,所以
,所以 ,即
,即 .
.
所以 为直角三角形. 12分
为直角三角形. 12分
考点:解三角形,两角和差公式
点评:主要是考查了运用两角和差的公式推理论证表达式以及运用二倍角公式来得到三角形定形,属于中档题。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
△ABC中,已知 60°,如果△ABC 有两组解,则x的取值范围( )
60°,如果△ABC 有两组解,则x的取值范围( )
A. | B. | C. | D. |
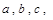 且对
且对 是常数,
是常数, .
. 的值;
的值; 且
且 ,求:
,求: 的值.
的值. <α<
<α< ,0<β<
,0<β< ,
, +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值. 为锐角,
为锐角, ,
, ,求
,求 的值.
的值. 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角 ,
, ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于 两点,已知点
两点,已知点 的横坐标为
的横坐标为 ,点
,点 的纵坐标为
的纵坐标为 .
. 的值;
的值; 的值.
的值. ,
, 、b、c,且
、b、c,且 ,若向量
,若向量 共线,求
共线,求 (2)
(2) .
.