题目内容

1．已知数列{an}的前n项和是Sn，若n＞1时，2an=an+1+an-1，且S3＜S5＜S4，则满足Sn-1Sn＜0（n＞1）的正整数n的值为9．

分析 可判断数列{an}是等差数列，且S5-S3=a4+a5＞0，S5-S4=a5＜0，从而求得S8=$\frac{{a}_{4}+{a}_{5}}{2}$×8＞0，S9=9a5＜0，从而解得．

解答 解：∵当n＞1时，2an=an+1+an-1，
∴数列{an}是等差数列，
∵S3＜S5＜S4，
∴S5-S3=a4+a5＞0，S5-S4=a5＜0，
∴数列{an}是递减的等差数列，
而S8=$\frac{{a}_{4}+{a}_{5}}{2}$×8＞0，
S9=9a5＜0，
故n=9，
故答案为：9

点评 本题考查了等差数列的判断与数列的性质的判断，同时考查了前n项和公式的应用．

练习册系列答案
相关题目
11．已知角α的终边经过点P（1，2），则tanα=2．
12．一个口袋内装有大小相同的红、蓝球各一个，若有放回地摸出一个球并记下颜色为一次试验，试验共进行三次，则至少摸到一次红球的概率是（　　）
A．$\frac{1}{8}$B．$\frac{7}{8}$C．$\frac{3}{8}$D．$\frac{5}{8}$
9．△ABC的三边a，b，c成等差数列，A、C两点的坐标分别是（-1，0），（1，0），求顶点B的轨迹方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1（x≠±2）．
16．已知函数f（x）=x2，数列{an}满足an+1=2f（an-1）+1，且a1=3，an＞1．
（1）设bn=log2（an-1），证明：数列{bn+1}是等比数列；
（2）求数列{bn}的前n项和Sn．
6．在△ABC中，角A，B，C的对边分别为a，b，c，且满足$cos\frac{A}{2}=\frac{{2\sqrt{5}}}{5}，\overrightarrow{AB}•\overrightarrow{AC}=15$．
（1）求△ABC的面积；
（2）若tanB=2，求a的值．
13．复数$\frac{{{i^{2017}}}}{1+i}$（其中i为虚数单位）的模等于$\frac{\sqrt{2}}{2}$．
10．函数f（x）=lnx-x的单调增区间为（　　）
A．（1，+∞）B．（0，1）C．（-∞，1）D．（0，+∞）
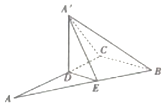11．如图，将直角△ABC沿着平行BC边的直线DE折起，使得平面A′DE⊥平面BCDE，其中D、E分别在AC、AB边上，且AC⊥BC，BC=3，AB=5，点A′为点A折后对应的点，当四棱锥A′-BCDE的体积取得最大值时，求AD的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网