题目内容
若数列{an}的前n项和Sn=2n.
(Ⅰ)求{an}的通项公式;
(Ⅱ)令bn=nan.求{bn}的前10项和.
(Ⅰ)求{an}的通项公式;
(Ⅱ)令bn=nan.求{bn}的前10项和.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由数列{an}的前n项和Sn=2n,利用an=
,能求出{an}的通项公式.
(Ⅱ)由an =
,bn=nan,知{bn}的前10项和T10=2+2•2+3•22+…+10•29,由此利用错位相减法能求出结果.
|
(Ⅱ)由an =
|
解答:
解:(Ⅰ)∵数列{an}的前n项和Sn=2n,
∴a1=S1=2,
当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,
当n=1时,2n-1=1≠a1,
∴an =
.
(Ⅱ)∵an =
,bn=nan,
∴{bn}的前10项和T10=2+2•2+3•22+…+10•29,①
2T10=2•2+2•22+3•23+…+10•210,②
②-①,得:T10=-2-22-23-…-29+10•210
=10•210-
=9•210+2
=9218.
∴a1=S1=2,
当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,
当n=1时,2n-1=1≠a1,
∴an =
|
(Ⅱ)∵an =
|
∴{bn}的前10项和T10=2+2•2+3•22+…+10•29,①
2T10=2•2+2•22+3•23+…+10•210,②
②-①,得:T10=-2-22-23-…-29+10•210
=10•210-
| 2(1-29) |
| 1-2 |
=9•210+2
=9218.
点评:本题考查数列的通项公式和前10项和的求法,解题时要认真审题,注意错位相减法的合理运用,是中档题.

练习册系列答案
相关题目
等比数列{an}满足an>0,n∈N+,且a3•a2n-3=22n(n≥2),则当n≥1时,log2a1+log2a2+…+log2a2n-1=( )
| A、n(2n-1) |
| B、(n+1)2 |
| C、n2 |
| D、(n-1)2 |
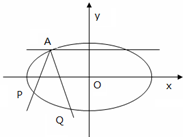 如图,焦点在x轴的椭圆,离心率e=
如图,焦点在x轴的椭圆,离心率e= 如图在四面体ABCD中,若截面PQMN是正方形,则在下列命题中正确的有
如图在四面体ABCD中,若截面PQMN是正方形,则在下列命题中正确的有