题目内容
【题目】向量集合![]() ,对于任意
,对于任意![]() ,以及任意
,以及任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“
为“![]() 类集”,现有四个命题:
类集”,现有四个命题:
①若![]() 为“
为“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
②若![]() ,
,![]() 都是“
都是“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
③若![]() 都是“
都是“![]() 类集”,则
类集”,则![]() 也是“
也是“![]() 类集”;
类集”;
④若![]() 都是“
都是“![]() 类集”,且交集非空,则
类集”,且交集非空,则![]() 也是“
也是“![]() 类集”.
类集”.
其中正确的命题有________(填所有正确命题的序号)
【答案】①②④
【解析】
因为集合![]() ,对于任意
,对于任意![]() ,且任意
,且任意![]() ,都有
,都有![]() ,可以把这个“
,可以把这个“![]() 类集”理解成,任意两个
类集”理解成,任意两个![]() 中的向量所表示的点的连线段上所表示的点都在
中的向量所表示的点的连线段上所表示的点都在![]() 上,因此可以理解它的图象成直线,逐项判断,即可求得答案.
上,因此可以理解它的图象成直线,逐项判断,即可求得答案.
![]() 集合
集合![]() ,对于任意
,对于任意![]() ,
,
且任意![]() ,都有
,都有![]()
![]() 可以把这个“
可以把这个“![]() 类集”理解成,任意两个
类集”理解成,任意两个![]() 中的向量所表示的点的连线段上所表示的点都在
中的向量所表示的点的连线段上所表示的点都在![]() 上,因此可以理解它的图象成直线
上,因此可以理解它的图象成直线
对于①,![]() ,向量
,向量![]() 整体
整体![]() 倍,还是表示的是直线,故①正确;
倍,还是表示的是直线,故①正确;
对于②,因为![]() ,
,![]() 都是“
都是“![]() 类集”,故
类集”,故![]() 还是表示的是直线,故②正确;
还是表示的是直线,故②正确;
对于③,因为![]() 都是“
都是“![]() 类集”,可得
类集”,可得![]() 是表示两条直线,故③错误;
是表示两条直线,故③错误;
对于④,![]() 都是“
都是“![]() 类集”,且交集非空,可得
类集”,且交集非空,可得![]() 表示一个点或者两直线共线时还是一条直线.
表示一个点或者两直线共线时还是一条直线.
综上所述,正确的是①②④.
故答案为:①②④.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某农场更新技术培育了一批新型的“盆栽果树”,这种“盆栽果树”将一改陆地栽植果树只在秋季结果的特性,能够一年四季都有花、四季都结果.现为了了解果树的结果情况,从该批果树中随机抽取了容量为120的样本,测量这些果树的高度(单位:厘米),经统计将所有数据分组后得到如图所示的频率分布直方图.
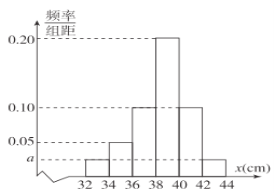
(1)求![]() ;
;
(2)已知所抽取的样本来自![]() 两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
(i)请将图中列联表补充完整,并判断是否有![]() 的把握认为“优品盆栽”与
的把握认为“优品盆栽”与![]() 两个实验基地有关?
两个实验基地有关?
优品 | 非优品 | 合计 | |
| 60 | ||
| 20 | ||
合计 |
(ii)用样本数据来估计这批果树的生长情况,若从该农场培育的这批“盆栽果树”中随机抽取4棵,求其中“优品盆栽”的棵树![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
![]() .
.