题目内容
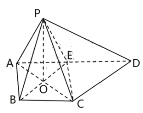
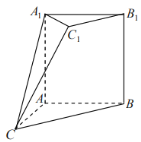
【题目】如图所示的几何体
中，四边形
是正方形，四边形
是梯形，
，且
，
，平面
平面ABC.
（1）求证：平面
平面；
（2）若
，
，求几何体的体积.
【答案】（1）证明见解析（2）
【解析】
（1）取BC的中点E，连接
，可证明
平面
，根据
可证明四边形
为平行四边形，从而可证
平面，进而证明平面
平面.（2）将所求几何体分割为四棱锥
和直三棱柱
两部分，通过四棱锥和棱柱的体积分别计算求和可得几何体的体积.
解：（1）取BC的中点E，连接，∵
，∴
∵
是正方形，∴
，又平面
平面ABC，∴
平面ABC，
又∵
平面ABC，∴
又∵
，
平面，
，∴平面
∵，∴四边形
为平行四边形，∴
，
∴四边形为平行四边形
∴
，∴平面
又
平面
，∴平面平面
（2）由（1）知所求几何体为四棱锥和直三棱柱的组合体
∵
，
，
，
平面，∴
平面，
∴四棱锥的体积
直三棱柱的体积
∴所求几何体
的体积
每日10分钟口算心算速算天天练系列答案【题目】随着移动互联网的发展，越来越多的人习惯用手机应用程序（简称app）获取新闻资讯.为了解用户对某款新闻类app的满意度，随机调查了300名用户，调研结果如表：（单位：人）
青年人 | 中年人 | 老年人 | |
满意 | 60 | 70 | x |
一般 | 55 | 25 | y |
不满意 | 25 | 5 | 10 |
（1）从所有参与调研的人中随机选取1人，估计此人“不满意”的概率；
（2）从参与调研的青年人和中年人中各随机选取1人，估计恰有1人“满意”的概率；
（3）现需从参与调研的老年人中选择6人作进一步访谈，若在“满意”、“一般”、“不满意”的老年人中各取2人，这种抽样是否合理？说明理由.
【题目】羽毛球比赛中，首局比赛由裁判员采用抛球的方法决定谁先发球，在每回合争夺中，赢方得1分且获得发球权．每一局中，获胜规则如下：①率先得到21分的一方赢得该局比赛；②如果双方得分出现
，需要领先对方2分才算该局获胜；③如果双方得分出现
，先取得30分的一方该局获胜．现甲、乙两名运动员进行对抗赛，在每回合争夺中，若甲发球时，甲得分的概率为
；乙发球时，甲得分的概率为
．
（Ⅰ）若
，记“甲以
赢一局”的概率为
，试比较
与
的大小；
（Ⅱ）根据对以往甲、乙两名运动员的比赛进行数据分析，得到如下
列联表部分数据．若不考虑其它因素对比赛的影响，并以表中两人发球时甲得分的频率作为，的值．
甲得分 | 乙得分 | 总计 | |
甲发球 | 50 | 100 | |
乙发球 | 60 | 90 | |
总计 | 190 |
①完成列联表，并判断是否有95%的把握认为“比赛得分与接、发球有关”？
②已知在某局比中，双方战成
，且轮到乙发球，记双方再战
回合此局比赛结束，求的分布列与期望．
参考公式：
，其中
．
临界值表供参考：
| 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
