题目内容
(文)数列{an}中a1=0,![]() ,(1)求证数列
,(1)求证数列![]() 为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设
为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设![]() ,证明:对任意正整数n,m,都有
,证明:对任意正整数n,m,都有![]() .
.
(1)略 (2)略
解析:
(1)∵![]() 即
即![]() ,∴公差d=-1.
,∴公差d=-1.
且首项为![]() ,故
,故![]() 是等差数列.
是等差数列.
(2)∵![]() ,∴
,∴![]() .
.
设f(x)=x-ln(x+1),(x>0),则![]() ,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴
,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴![]() ,即
,即![]() .
.
∴an<1-ln(n+1)+lnn,∴Sn<(1-ln2+ln1)+(1-ln3+ln2)+…+[1-ln(n+1)+lnn]=n-ln(n+1)故Sn<n-ln(n+1).
(3)∵![]() ,∴
,∴![]() ,当
,当![]() 时,则
时,则![]() ,∴
,∴![]() ,
,
即n≥4;又当![]() 时,则
时,则![]() ,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有
,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有![]()

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
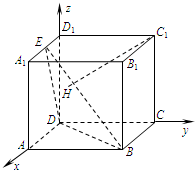 [理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,
[理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,