题目内容
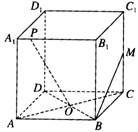
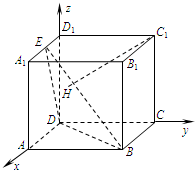 [理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,
[理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,| HC1 |
(1)证明HC1⊥平面EDB;
(2)求BC1与平面EDB所成的角;
(3)若正方体的棱长为a,求三棱锥A-EDB的体积.
[文]若数列{an}的通项公式an=
| 1 |
| (n+1)2 |
(1)计算f(1),f(2),f(3)的值;
(2)由(1)推测f(n)的表达式;
(3)证明(2)中你的结论.
分析:[理](1)由向量的数量积可得
•
=0 ,
•
=0,可得HC1⊥DE,HC1⊥DB,即由线线垂直得到线面垂直.
(2)由题意得面EDB的垂线是BC1,即平面的法向量
={ -a ,0 , a },进而求
与
所成的角θ即可.
(3)由于三棱锥A-EDB的体积不易求出,把三棱锥换一个顶点求三棱锥E-ABD的体积,高是AA1,底面为S△ABD
[文](1)将1,2,3分别代入数列{an}的通项公式an=
(n∈N+)计算f(1),f(2),f(3)的值即可.
(2)f(1)=1-a1=
f(2)=
,f(3)=
,f(4)=
,可以发现n与函数f(n)的关系f(n)的表示式.
(3)防写出所求的式子的类似的式子,把所写出的式子相乘,化简整理得到所写出的结果,结论正确.
| HC1 |
| DE |
| HC1 |
| DB |
(2)由题意得面EDB的垂线是BC1,即平面的法向量
| BC1 |
| BC1 |
| HC1 |
(3)由于三棱锥A-EDB的体积不易求出,把三棱锥换一个顶点求三棱锥E-ABD的体积,高是AA1,底面为S△ABD
[文](1)将1,2,3分别代入数列{an}的通项公式an=
| 1 |
| (n+1)2 |
(2)f(1)=1-a1=
| 3 |
| 4 |
| 2 |
| 3 |
| 5 |
| 8 |
| 3 |
| 5 |
(3)防写出所求的式子的类似的式子,把所写出的式子相乘,化简整理得到所写出的结果,结论正确.
解答:[理]解:(1)设正方体的棱长为a,
则
={
, 0 , a },
={ a , a , 0 },
∵
•
=0 ,
•
=0,
∴
⊥
,
⊥
,又DE∩DB=D,
∴HC1⊥平面EDB.
(2)
={ -a ,0 , a },
设
与
所成的角为θ,
cosθ=
=
=
∴θ=45°.
由(1)知HC1⊥平面EDB,
∴∠C1BH为BC1与平面EDB所成的角.
∠C1BH=90°-45°=45°.
(3)VA-EDB=VE-ABD=
•
a2•a=
a3
[文]解:(1)a1=
,a2=
,a3=
,a4=
,f(1)=1-a1=
f(2)=(1-a1)(1-a2)=
,
f(3)=(1-a1)(1-a2)(1-a3)=
,f(4)=(1-a1)(1-a2)(1-a3)(1-a4)=
,
(2)故猜想f(n)=
(n∈N*)
(3)证明:1-an=1-
=
=
•
1-an-1=
•
1-an-2=
•
1-an-3=
•
…1-a3=
•
1-a2=
•
1-a1=
•
将上述n个因式相乘得:(1-a1)(1-a2)(1-an)=
•
=
即f(n)=
(n∈N*)
则
| DE |
| a |
| 2 |
| DB |
∵
| HC1 |
| DE |
| HC1 |
| DB |
∴
| HC1 |
| DE |
| HC1 |
| DB |
∴HC1⊥平面EDB.
(2)
| BC1 |
设
| BC1 |
| HC1 |
cosθ=
| ||||
|
|
| 2ma+ma | ||
|
| ||
| 2 |
∴θ=45°.
由(1)知HC1⊥平面EDB,
∴∠C1BH为BC1与平面EDB所成的角.
∠C1BH=90°-45°=45°.
(3)VA-EDB=VE-ABD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
[文]解:(1)a1=
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 1 |
| 25 |
| 3 |
| 4 |
| 2 |
| 3 |
f(3)=(1-a1)(1-a2)(1-a3)=
| 5 |
| 8 |
| 3 |
| 5 |
(2)故猜想f(n)=
| n+2 |
| 2(n+1) |
(3)证明:1-an=1-
| 1 |
| (n+1)2 |
| n2+2n |
| (n+1)2 |
| n+2 |
| n+1 |
| n |
| n+1 |
1-an-1=
| n+1 |
| n |
| n-1 |
| n |
1-an-2=
| n |
| n-1 |
| n-2 |
| n-1 |
1-an-3=
| n-1 |
| n-2 |
| n-3 |
| n-2 |
| 5 |
| 4 |
| 3 |
| 4 |
1-a2=
| 4 |
| 3 |
| 2 |
| 3 |
1-a1=
| 3 |
| 2 |
| 1 |
| 2 |
将上述n个因式相乘得:(1-a1)(1-a2)(1-an)=
| n+2 |
| n+1 |
| 1 |
| 2 |
| n+2 |
| 2(n+1) |
即f(n)=
| n+2 |
| 2(n+1) |
点评:本题是两个题目,一个适合文科做,一个适合理科做,第一个题目解题的关键是建立坐标系,在坐标系里解决立体几何题目,第二个题目是猜测证明的一个过程,注意根据所给的几项的值写出数列的通项,并且加以证明.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目