题目内容
5．设$\underset{lim}{x→-1}$$\frac{{x}^{3}-a{x}^{2}-x+4}{x+1}$有极限A，求a，A．分析 先分析出该极限是一个“$\frac{0}{0}$”型极限，从而确定a的值，再对分子因式分解，化简后再求其极限．
解答 解：当x→-1时，分母x+1→0，
且原式极限存在，所以该极限是“$\frac{0}{0}$”型极限，
因此，当x=-1时，分子等于零，
即-1-a+1+4=0，解得a=4，所以，
原式=$\underset{lim}{x→-1}$$\frac{x^3-4x^2-x+4}{x+1}$
=$\underset{lim}{x→-1}$$\frac{（x+1）（x-1）（x-4）}{x+1}$
=$\underset{lim}{x→-1}$（x-1）（x-4）
=（-2）×（-5）=10，
所以，a=4，A=10．
点评 本题主要考查了极限及其运算，尤其是要分析出该极限是“$\frac{0}{0}$”型极限，考查了多项式的因式分解，属于中档题．
练习册系列答案
相关题目
16．已知函数y=lgx的定义域为集合A，集合B={0，1，2}，则A∩B=（ ）
| A． | （0，+∞） | B． | （0，2] | C． | {0，1，2} | D． | {1，2} |
已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$，半径OA=1，在$\widehat{AB}$上有一个动点M，过M作矩形MNPQ，如图，设∠AOM=θ，记矩形MNPQ的面积为S．
20．
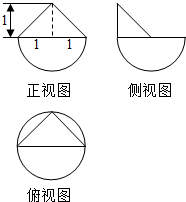某几何体的三视图如图所示，则该几何体的表面积为（ ）
某几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | 3π+2$\sqrt{2}$-1 | B． | 3π+2$\sqrt{2}$ | C． | 2π+2$\sqrt{2}$-1 | D． | 2π+2$\sqrt{2}$ |
