题目内容
20.数列{an}前n项和Sn=3n-1,(1)试写出数列的前4项,
(2)数列{an}是等比数列吗?
(3)求出数列的通项公式.
分析 (1)在数列的前n项和公式中,分别取n=1,2,3,4,结合an=Sn-Sn-1求得数列的前4项;
(2)求出数列的通项公式,由等比数列的定义证明数列是等比数列;
(3)直接由(2)得答案.
解答 解:(1)由Sn=3n-1,
得a1=S1=2,a2=S2-S1=6,a3=S3-S2=18,a4=S4-S3=54;
(2)当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}={3}^{n}-1-({3}^{n-1}-1)=2•{3}^{n-1}$,
验证n=1时,上式成立,
∴${a}_{n}=2•{3}^{n-1}$,
由$\frac{{a}_{n+1}}{{a}_{n}}=\frac{2•{3}^{n}}{2•{3}^{n-1}}=3$(常数),可得数列{an}是等比数列;
(3)由(2)可得${a}_{n}=2•{3}^{n-1}$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了由数列的前n项和求得数列的通项公式,是中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
12.椭圆C的焦点在x轴上,一个顶点坐标是(2,0),过焦点且垂直于长轴的弦长为1,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{14}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
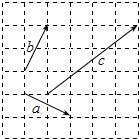 如图,在6×6的方格中,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$的起点和终点均在格点,且满足向量$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),那么x+y=3.
如图,在6×6的方格中,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$的起点和终点均在格点,且满足向量$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),那么x+y=3.