题目内容
已知向量 =(tanx,1),
=(tanx,1), =(sinx,cosx),其中
=(sinx,cosx),其中 =
= •
• .
.
(I)求函数f(x)的解析式及最大值;
(II)若 ,求
,求 的值.
的值.
解:(I)∵ =(tanx,1),
=(tanx,1), =(sinx,cosx),
=(sinx,cosx),
∴f(x)= •
• =
= .
.
∵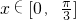 ,∴当
,∴当 时,f(x)的最大值为
时,f(x)的最大值为 .
.
(II)∵ ,∴
,∴ .
.
∵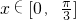 ,∴
,∴ .
.
 =
= =
= =-sin2x=-2sinxcosx=
=-sin2x=-2sinxcosx= .
.
分析:(I)利用向量的坐标和向量积的运算,化简整理求得函数f(x)的解析式.利用余弦函数的性质可在x= 时函数有最大值.
时函数有最大值.
(II)利用 求得cosx的值,进而利用同角三角函数基本关系求得sinx的值,利用诱导公式和二倍角公式对原式化简整理,把sinx和cosx的值代入即可.
求得cosx的值,进而利用同角三角函数基本关系求得sinx的值,利用诱导公式和二倍角公式对原式化简整理,把sinx和cosx的值代入即可.
点评:本题主要考查了三角函数的最值,同角三角函数基本关系的应用,诱导公式和二倍角公式的化简求值.综合考查了学生基础知识运用.
 =(tanx,1),
=(tanx,1), =(sinx,cosx),
=(sinx,cosx),∴f(x)=
 •
• =
= .
.∵
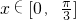 ,∴当
,∴当 时,f(x)的最大值为
时,f(x)的最大值为 .
.(II)∵
 ,∴
,∴ .
.∵
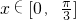 ,∴
,∴ .
. =
= =
= =-sin2x=-2sinxcosx=
=-sin2x=-2sinxcosx= .
.分析:(I)利用向量的坐标和向量积的运算,化简整理求得函数f(x)的解析式.利用余弦函数的性质可在x=
 时函数有最大值.
时函数有最大值.(II)利用
 求得cosx的值,进而利用同角三角函数基本关系求得sinx的值,利用诱导公式和二倍角公式对原式化简整理,把sinx和cosx的值代入即可.
求得cosx的值,进而利用同角三角函数基本关系求得sinx的值,利用诱导公式和二倍角公式对原式化简整理,把sinx和cosx的值代入即可.点评:本题主要考查了三角函数的最值,同角三角函数基本关系的应用,诱导公式和二倍角公式的化简求值.综合考查了学生基础知识运用.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
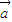 =(1-tanx,1),
=(1-tanx,1),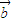 =(1+sin2x+cos2x,-3),记f(x)=
=(1+sin2x+cos2x,-3),记f(x)=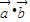
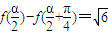 ,其中
,其中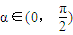 ,求角α.
,求角α.