题目内容
已知 是
是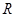 上的奇函数,且当
上的奇函数,且当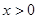 时,
时,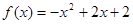 .
.
(1)求 的表达式;
的表达式;
(2)画出 的图象,并指出
的图象,并指出 的单调区间.
的单调区间.
(1) 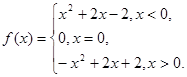 ;
;
(2)由图可知,其增区间为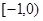 和
和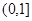 ,减区间为
,减区间为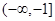 和
和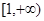 .
.
解析试题分析:(1)根据 是定义在
是定义在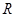 上的奇函数,先设
上的奇函数,先设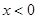 时,则
时,则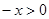 ,结合题意得到
,结合题意得到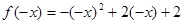 ,然后利用函数的奇偶性进行化简,进而得到函数的解析式.
,然后利用函数的奇偶性进行化简,进而得到函数的解析式.
(2)先画出当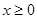 时的函数图象,结合奇函数图象关于原点对称可画出
时的函数图象,结合奇函数图象关于原点对称可画出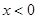 时的函数图象即可.
时的函数图象即可.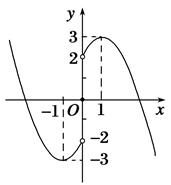
(3)结合函数的图象进行判断.
(1) 设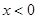 时,则
时,则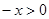 ,
,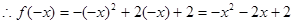 .
.
又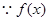 为奇函数,
为奇函数,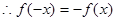 .
.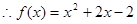 .
.
又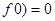 ,
,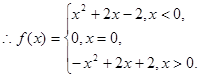
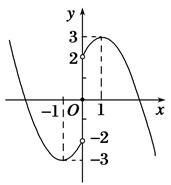
(2)先画出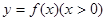 的图象,利用奇函数的对称性可得到相应
的图象,利用奇函数的对称性可得到相应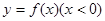 的图象,其图象如右图所示.由图可知,其增区间为
的图象,其图象如右图所示.由图可知,其增区间为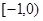 和
和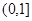 ,减区间为
,减区间为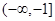 和
和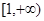 .
.
考点:函数的零点与方程根的关系;奇偶性与单调性的综合.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
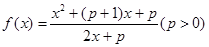 和
和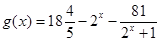 的定义域都是[2,4].
的定义域都是[2,4].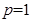 ,求
,求 的最小值;
的最小值;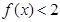 在其定义域上有解,求
在其定义域上有解,求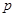 的取值范围;
的取值范围;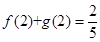 ,求证
,求证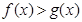 .
.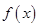 是定义在
是定义在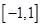 上的奇函数,在
上的奇函数,在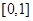 上
上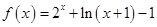 .
.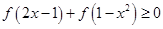 .
. 是
是 上的增函数,
上的增函数,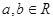 ,且
,且 ,求证
,求证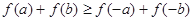
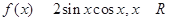 .
. 的最小正周期;
的最小正周期;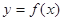 的奇偶性, 并说明理由。
的奇偶性, 并说明理由。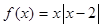 .
.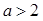 ,求
,求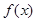 在
在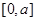 上的最大值.
上的最大值. a为常数且a>0.
a为常数且a>0. 对称;
对称;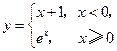 的反函数是__________.
的反函数是__________.