题目内容
已知函数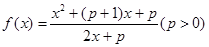 和
和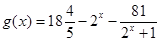 的定义域都是[2,4].
的定义域都是[2,4].
若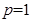 ,求
,求 的最小值;
的最小值;
若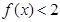 在其定义域上有解,求
在其定义域上有解,求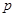 的取值范围;
的取值范围;
若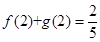 ,求证
,求证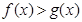 .
.
(1) 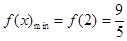 ; (2)
; (2) 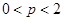 ; (3) 祥见解析.
; (3) 祥见解析.
解析试题分析:(1)将p=1代入函数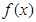 知其为分式函数,而又知其定义域为[2,4],所以我们可用导数方法来判断函数的单调性,进而就可求出其最小值;
知其为分式函数,而又知其定义域为[2,4],所以我们可用导数方法来判断函数的单调性,进而就可求出其最小值;
试题解析:(1)将p=1代入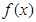 中,所以
中,所以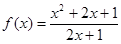 ,所以f(x)的导数为
,所以f(x)的导数为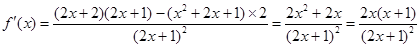 ,令
,令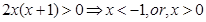
所以 当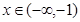 和
和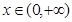 时函数
时函数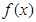 为增函数,又因为已知定义域为[2,4],所以
为增函数,又因为已知定义域为[2,4],所以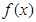 恒为增函数,所以
恒为增函数,所以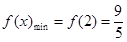 ;
;
(2)令k=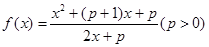
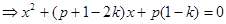 ,要求f(x)<2在定义域上有解,则方程
,要求f(x)<2在定义域上有解,则方程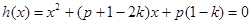 当k<2时在[2,4]上有解,∵k<2,p>0
当k<2时在[2,4]上有解,∵k<2,p>0
∴抛物线对称轴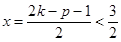 ,从而方程
,从而方程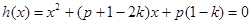 ,当k<2时在[2,4]上有解
,当k<2时在[2,4]上有解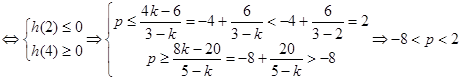 ,又p>0,∴0<p<2;
,又p>0,∴0<p<2;
(3)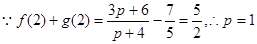 ;根据第(1)问结论:
;根据第(1)问结论: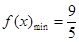
而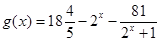
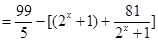 ,
,
∵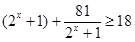 ,当且仅当x=3时取等号;∴
,当且仅当x=3时取等号;∴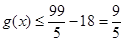 ,而
,而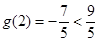
∴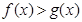 .
.
考点:1.函数的最值;2.函数的零点;3.基本不等式.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
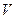 是已知平面
是已知平面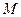 上所有向量的集合,对于映射
上所有向量的集合,对于映射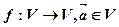 ,记
,记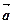 的象为
的象为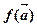 。若映射
。若映射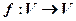 满足:对所有
满足:对所有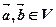 及任意实数
及任意实数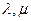 都有
都有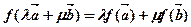 ,则
,则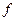 称为平面
称为平面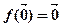
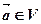 设
设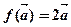 ,则
,则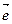 是平面
是平面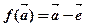 ,则
,则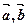 共线,则
共线,则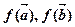 也共线。
也共线。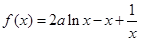 (
( 且
且 ),
),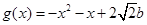
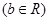 .
. 在定义域上有极值,求实数
在定义域上有极值,求实数 的取值范围;
的取值范围;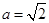 时,若对
时,若对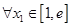 ,总
,总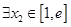 ,使得
,使得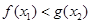 ,求实数
,求实数 的取值范围;(其中
的取值范围;(其中 为自然对数的底数)
为自然对数的底数)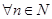 ,且
,且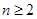 ,证明:
,证明: 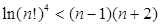 .
.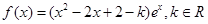 。
。 上的最小值为e,求k的值。
上的最小值为e,求k的值。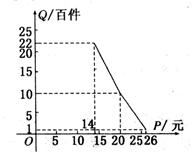
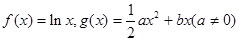 .
.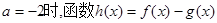 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;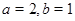 ,若函数
,若函数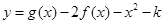 在 [1,3]上恰有两个不同零点,求实数
在 [1,3]上恰有两个不同零点,求实数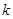 的取值范围.
的取值范围. 是
是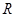 上的奇函数,且当
上的奇函数,且当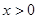 时,
时,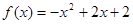 .
. 是奇函数.
是奇函数.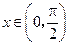 ,则函数
,则函数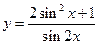 的最小值为 .
的最小值为 .