题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]()
![]() 到焦点
到焦点![]() 的距离等于
的距离等于![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() 在抛物线
在抛物线![]() 上且异于原点,点
上且异于原点,点![]() 为直线
为直线![]() 上的点,且
上的点,且![]() .求直线
.求直线![]() 与抛物线
与抛物线![]() 的交点个数,并说明理由.
的交点个数,并说明理由.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 与抛物线
与抛物线![]() 只有一个交点,理由见解析。
只有一个交点,理由见解析。
【解析】
(1)由题意,的奥抛物线的准线方程为![]() ,列出方程,求得
,列出方程,求得![]() 的值,即可得到答案.
的值,即可得到答案.
(2)设点![]() 为
为![]() ,点
,点![]() 为
为![]() ,焦点
,焦点![]() 为
为![]() ,由题意可得
,由题意可得![]() ,列出方程,得到直线
,列出方程,得到直线![]() 的方程,再与抛物线方程联立,即可求解.
的方程,再与抛物线方程联立,即可求解.
(1)抛物线的准线方程为![]() ,
,
所以点![]()
![]() 到焦点的距离为
到焦点的距离为![]() .
.
解得![]() .
.
所以抛物线![]() 的方程为
的方程为![]() .
.
(2)直线![]() 与抛物线
与抛物线![]() 只有一个交点,理由如下:
只有一个交点,理由如下:
设点![]() 为
为![]() ,点
,点![]() 为
为![]() ,焦点
,焦点![]() 为
为![]() .
.
则![]() ,
,![]() .
.
由题意可得![]() ,
,
故![]() .
.
从而![]() .
.
故直线![]() 的斜率
的斜率 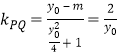 .
.
故直线![]() 的方程为
的方程为![]() ,即
,即![]() .①
.①
又抛物线![]() 的方程
的方程![]() ,②
,②
联立消去![]() 得
得 ![]() ,故
,故![]() ,且
,且![]() .
.
故直线![]() 与抛物线
与抛物线![]() 只有一个交点.
只有一个交点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目