Question

（文科）双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的左、右焦点分别为F₁、F₂，过点 F₁作倾斜角为30°的直线l，l与双曲线的右支交于点P，若线段PF₁的中点M落在y轴上，则双曲线的渐近线方程为（　　）

• A．y=±x
• B．y=±

  3

  x
• C．y=±

  2

  x
• D．y=±2x

Answer 1

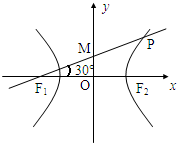
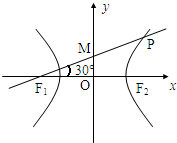
分析：由于线段PF₁的中点M落在y轴上，连接MF₂，则|MF₁|=|MF₂|=|PM|=

1

2

|PF₁|⇒△PF₁F₂为直角三角形，△PMF₂为等边三角形，于是|PF₁|-|PF₂|=|MF₁|=2a，|F₁F₂|=2c=

3

|MF₁|=2

3

a⇒c=

3

a，由c²=a²+b²可求得b=

2

a，于是 双曲线的渐近线方程可求．

解答：解：连接MF₂，由过点 PF₁作倾斜角为30°，线段PF₁的中点M落在y轴上得：|MF₁|=|MF₂|═|PM|=

1

2

|PF₁|，
∴△PMF₂为等边三角形，△PF₁F₂为直角三角形，
∵是|PF₁|-|PF₂|=|MF₁|=2a，|F₁F₂|=2c=

3

|MF₁|=2

3

a
∴c=

3

a，又c²=a²+b²，
∴3a²=a²+b²，
∴b=

2

a，
∴双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的渐近线方程为：y=±

b

a

x=±

2

x．   
故选 C．

点评：本题考查直线与圆锥曲线的位置关系，关键是对双曲线定义的灵活应用及对三角形△PMF₂为等边三角形，△PF₁F₂为直角三角形的分析与应用，属于难题．