题目内容
14.已知0<x<$\frac{π}{2}$,且tan(x-$\frac{π}{4}$)=-$\frac{1}{7}$,则sinx+cosx=$\frac{7}{5}$.分析 利用两角差的正切公式求出tanx的值,又根据已知条件列出方程组,求解即可得到sinx,cosx的值,代入sinx+cosx计算得答案.
解答 解:∵tan(x-$\frac{π}{4}$)=-$\frac{1}{7}$,
∴$\frac{tanx-1}{1+tanx}$=$-\frac{1}{7}$,则tanx=$\frac{3}{4}$
又0<x<$\frac{π}{2}$,
∴$\left\{\begin{array}{l}{\frac{sinx}{cosx}=\frac{3}{4}}\\{si{n}^{2}x+co{s}^{2}x=1}\end{array}\right.$,解得sinx=$\frac{3}{5}$,cosx=$\frac{4}{5}$,
则sinx+cosx=$\frac{3}{5}+\frac{4}{5}=\frac{7}{5}$.
故答案为:$\frac{7}{5}$.
点评 本题考查了同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键,是基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
5.若a>b>c,a+b+c=0,则下列各是正确的是( )
| A. | ab>ac | B. | ac>bc | C. | a|b|>|b|c | D. | ab>bc |
9.在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( )
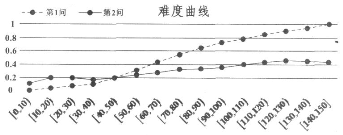

| A. | 此题没有考生得12分 | |
| B. | 此题第1问比第2问更能区分学生数学成绩的好与坏 | |
| C. | 分数在[40,50)的考生此大题的平均得分大约为4.8分 | |
| D. | 全体考生第1问的得分标准差小于第2问的得分标准差 |
6.关于函数f(x)=x3-3x2+6x的单调性是( )
| A. | 增函数 | B. | 先增后减 | C. | 先减后增 | D. | 减函数 |
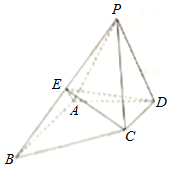 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点