题目内容
设函数f(x)=[x]-1,x∈(0,+∞)(其中[x]表示不超过x的最大整数,如[
]=0,[
]=1,[2]=2),则方程f(x)-log2x=0的根的个数是( )
| 1 |
| 3 |
| 6 |
| 3 |
| A、1 | B、2 | C、3 | D、无数个 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由方程f(x)-log2x=0,得程f(x)=log2x,然后根据定义分别讨论f(x)的表达式,利用数形结合即可得到结论.
解答:
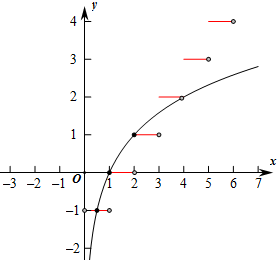 解:由方程f(x)-log2x=0,得程f(x)=log2x,
解:由方程f(x)-log2x=0,得程f(x)=log2x,
当0<x<1,[x]=0,则f(x)=[x]-1=-1,此时log2x<0,由f(x)=log2x=-1,解得x=
,
当1≤x<2,[x]=1,则f(x)=[x]-1=1-1=0,由f(x)=log2x=0,解得x=1,满足条件,
当2≤x<3,[x]=2,则f(x)=[x]-1=2-1=1,由f(x)=log2x=1,解得x=2,满足条件,
当3≤x<4,[x]=3,则f(x)=[x]-1=3-1=2,由f(x)=log2x=2,解得x=4,不满足条件,
当4≤x<5,[x]=4,则f(x)=[x]-1=4-1=3,此时log2x<3,此时方程无解,不满足条件,
…
当n≤x<n+1,(n≥5),[x]=,n,则f(x)=[x]-1=n-1=3,此时方程无解,不满足条件,
故方程f(x)-log2x=0的根的个数是3个.
故选:C
 解:由方程f(x)-log2x=0,得程f(x)=log2x,
解:由方程f(x)-log2x=0,得程f(x)=log2x,当0<x<1,[x]=0,则f(x)=[x]-1=-1,此时log2x<0,由f(x)=log2x=-1,解得x=
| 1 |
| 2 |
当1≤x<2,[x]=1,则f(x)=[x]-1=1-1=0,由f(x)=log2x=0,解得x=1,满足条件,
当2≤x<3,[x]=2,则f(x)=[x]-1=2-1=1,由f(x)=log2x=1,解得x=2,满足条件,
当3≤x<4,[x]=3,则f(x)=[x]-1=3-1=2,由f(x)=log2x=2,解得x=4,不满足条件,
当4≤x<5,[x]=4,则f(x)=[x]-1=4-1=3,此时log2x<3,此时方程无解,不满足条件,
…
当n≤x<n+1,(n≥5),[x]=,n,则f(x)=[x]-1=n-1=3,此时方程无解,不满足条件,
故方程f(x)-log2x=0的根的个数是3个.
故选:C
点评:本题主要考查方程根的个数以及[x]的应用,利用分段函数求出f(x)的表达式,以及利用数形结合是解决本题的关键.综合性较强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
i是虚数单位,复数
对应的点在( )
| 7-i |
| 3+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知F1,F2是双曲线C1:
-
=1(a>0,b>0)与椭圆C2:
+
=1的公共焦点,A、B是两曲线分别在第一、三象限的交点,且以F1、F2、A、B为顶点的四边形的面积为6
,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 9 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若奇函数f(x)在R上为增函数,a、b、c∈R,则“a+b>0,b+c>0,c+a>0”是“f(a)+f(b)+f(c)>0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设P={x|x≥0},Q={x|-1≤x<2},那么P∪Q=( )
| A、{x|}{x|x≤-1或x≥0} |
| B、{x|x≤-1或x≥2} |
| C、{x|x≥-1} |
| D、{x|0≤x<2} |
为了得到函数y=sin(2x+
)的图象,只需把函数y=sin(2x-
)的图象( )
| π |
| 3 |
| π |
| 6 |
A、向右平移个
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
| 1-i2 |
| 1+i |
| A、i | B、-i | C、1+i | D、1-i |