题目内容
设函数![]() 求证:
求证:
(Ⅰ)![]() ;
;
(Ⅱ)函数![]() 在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点;
(Ⅲ)设![]() 是函数
是函数![]() 的两个零点,则
的两个零点,则![]()
证明:(Ⅰ)![]()
![]()
又![]()
![]()
![]()
又2c=-3a-2b 由3a>2c>2b ∴3a>-3a-2b>2b
∵a>0 ![]()
(Ⅱ)∵f(0)=c,f(2)=4a+2b+c=a-c
①当c>0时,∵a>0,∴f(0)=c>0且![]()
∴函数f(x)在区间(0,1)内至少有一个零点
②当c≤0时,∵a>0 ![]()
∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点
(Ⅲ)∵x1,x2是函数f(x)的两个零点
则![]() 的两根
的两根
∴![]()
![]()
![]()
![]()

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
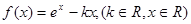
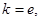 试确定函数
试确定函数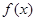 的单调区间;
的单调区间;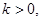 且对于任意
且对于任意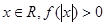 恒成立,试确定实数
恒成立,试确定实数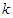 的取值范围;
的取值范围; 求证:
求证: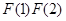
 .
.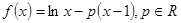 .
.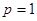 时,求函数
时,求函数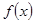 的单调区间;
的单调区间;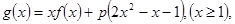 求证:当
求证:当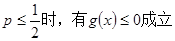
 求证:
求证: ;
;  在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点;