题目内容
设函数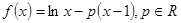 .
.
(Ⅰ)当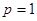 时,求函数
时,求函数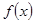 的单调区间;
的单调区间;
(Ⅱ)设函数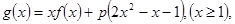 求证:当
求证:当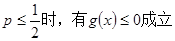
【答案】
(I)当p =1时, ,其定义域为
,其定义域为 .
.
所以 .
…………2分
.
…………2分
由 得
得 ,
,
所以 的单调增区间为
的单调增区间为 ;单调减区间为
;单调减区间为 .………5分
.………5分
(II)由函数 ,
,
得 …………7分
…………7分
由(I)知,当p =1时, ,
,
即不等式 成立.
…………9分
成立.
…………9分
所以当 时,
时, ,
,
即g(x)在 上单调递减,
上单调递减,
从而 满足题意.
满足题意.
【解析】略

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
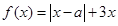 ,其中
,其中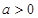 。
。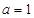 时,求不等式
时,求不等式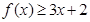 的解集;
的解集;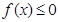 的解集为
的解集为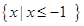 ,求a的值。
,求a的值。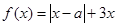 ,其中
,其中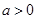 。
。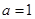 时,求不等式
时,求不等式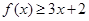 的解集;
的解集;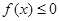 的解集为
的解集为 ,求a的值。
,求a的值。