题目内容
18.已知函数y=$\sqrt{{x}^{2}-2x+a}$的定义域为R,值域为[0,+∞),则实数a的取值集合为{1}.分析 本题可以由函数的值域得到函数解析式满足条件,从而求出实数a的取值范围,得到本题结论
解答 解:记f(x)=x2-2x+a,
∵函数y=$\sqrt{{x}^{2}-2x+a}$的定义域为R,值域为[0,+∞),
则f(x)=ax2+2ax+1的图象是抛物线,开口向上,顶点在x轴上,
∴a>0,且△=4-4a=0,
∴a=1.
∴实数a的取值集合是:{1}.
故答案为:{1}.
点评 本题考查了函数的值域和内函数图象的关系,主要考查二次函数的性质,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知x>1,y>1,log2x+log2y=log2(x+y),log2x+log2y+log2z=log2(x+y+z),则z的范围为( )
| A. | [1,$\frac{4}{3}$) | B. | (1,$\frac{4}{3}$) | C. | (1,$\frac{4}{3}$] | D. | [--$\frac{4}{3}$] |
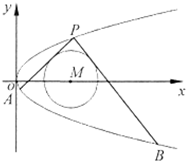 已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.
已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.