题目内容
2.${(\frac{1}{9})^{-1+{{log}_3}4}}+lg\frac{5}{2}+2lg2-{(\frac{1}{2})^{-1}}$的值为-$\frac{7}{16}$.分析 根据对数和指数的运算性质计算即可.
解答 解:${(\frac{1}{9})^{-1+{{log}_3}4}}+lg\frac{5}{2}+2lg2-{(\frac{1}{2})^{-1}}$=32÷${3}^{lo{g}_{3}16}$+lg5-lg2+2lg2-2=32÷${3}^{lo{g}_{3}16}$+lg5+lg2-2=9÷16+1-2=-$\frac{7}{16}$,
故答案为:-$\frac{7}{16}$.
点评 本题考查了对数和指数的运算性质,属于基础题.

练习册系列答案
相关题目
16.函数f(x)=3sin(x+$\frac{π}{6}$)+$\sqrt{3}$sin($\frac{π}{3}$-x)的最大值是( )
| A. | 3 | B. | 6 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
10.若cos2θ+cosθ=0,则sin2θ+sinθ的值等于( )
| A. | 0 | B. | ±$\sqrt{3}$ | C. | 0或$\sqrt{3}$ | D. | 0或±$\sqrt{3}$ |
7.一个三棱锥的三视图如图所示,则该三棱锥的表面积为( )
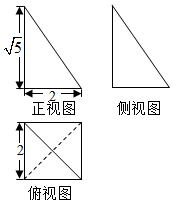

| A. | 8+$\sqrt{14}$ | B. | 8+2$\sqrt{14}$ | C. | 2+2$\sqrt{5}$+$\sqrt{14}$ | D. | 16+2$\sqrt{14}$ |