题目内容
17.若(x+$\frac{1}{2x}$)n的展开式中前3项的系数成等差数列,则其展开式中所有项的二项式系数之和是( )| A. | 28 | B. | 27 | C. | 1 | D. | 0 |
分析 利用二项式展开式的通项公式求出展开式中前3项的系数,再根据它们成等差数列求得n的值,可得展开式中所有项的二项式系数之和为2n的值.
解答 解:∵(x+$\frac{1}{2x}$)n的展开式中前3项的系数分别为1,$\frac{1}{2}$n,${C}_{n}^{2}$•${(\frac{1}{2})}^{2}$,
根据它们成等差数列,可得1+${C}_{n}^{2}$•${(\frac{1}{2})}^{2}$=n,∴n=8,
则其展开式中所有项的二项式系数之和为2n=28,
故选:A.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
8.已知函数f(x)=x2+mx+n,且y=f(x+2)的图象关于y轴对称,则大小关系正确的是( )
| A. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | B. | f(1)<f($\frac{7}{2}$)<f($\frac{5}{2}$) | C. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | D. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) |
2.某用水量较大的企业为积极响应政府号召的“节约用水,我们共同的责任”的倡议,对生产设备进行技术改造,下表提供了该企业节约用水技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产用水y(吨)的几组对照数据:
(1)若x,y之间是线性相关,请根据表中提供的数据,求y关于x的线性回归方程y=bx+a;
(2)已知该厂技术改造前100吨甲产品的生产用水为120吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨甲产品的用水量比技术改造前减少了多少吨?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
| x | 1 | 2 | 3 | 4 |
| y | 0.4 | 0.9 | 1.1 | 1.6 |
(2)已知该厂技术改造前100吨甲产品的生产用水为120吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨甲产品的用水量比技术改造前减少了多少吨?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
6.已知平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,$\overrightarrow{a}=(1,1)$,$\overrightarrow{a}+3\overrightarrow{b}=(4,-2)$,则cosθ=( )
| A. | 0 | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
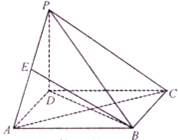 如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,
如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,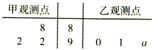 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.