题目内容
设函数f(x)=ln x-ax,g(x)=ex-ax,其中a为实数.
若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围.
解:令f′(x)= -a=
-a= <0,考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a-1,即f(x)在(a-1,+∞)上是单调减函数.
<0,考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a-1,即f(x)在(a-1,+∞)上是单调减函数.
同理,f(x)在(0,a-1)上是单调增函数.由于f(x)在(1,+∞)上是单调减函数,故(1,+∞)⊆(a-1,+∞),从而a-1≤1,即a≥1.令g′(x)=ex-a=0,得x=ln a.当x<ln a时,g′(x)<0;当x>ln a时,g′(x)>0.又g(x)在(1,+∞)上有最小值,所以ln a>1,即a>e.
综上,a的取值范围为(e,+∞).

练习册系列答案
相关题目
 (t是时间,s是位移),则物体在时刻t=2时的速度为( )
(t是时间,s是位移),则物体在时刻t=2时的速度为( ) B.
B.
 D.
D.
 x3-
x3- x2+ax+4恰在[-1,4]上单调递减,则实数a的值为________.
x2+ax+4恰在[-1,4]上单调递减,则实数a的值为________.
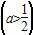 ,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )
,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )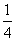 B.
B.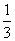
 D.1
D.1 -u与
-u与 2成正比,且售价为10元时,年销量为28万件.
2成正比,且售价为10元时,年销量为28万件. =( )
=( ) ,tan α=
,tan α= ,求tan 2α和sin
,求tan 2α和sin 的值.
的值.