题目内容
(本小题满分15分)已知函数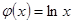
(Ⅰ)若曲线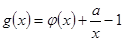 在点
在点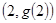 处的切线与直线
处的切线与直线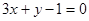 平行,求
平行,求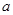 的值;
的值;
(Ⅱ)记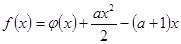 ,
, ,且
,且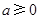 .求函数
.求函数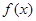 的单调递增区间.
的单调递增区间.
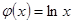
(Ⅰ)若曲线
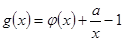 在点
在点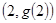 处的切线与直线
处的切线与直线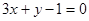 平行,求
平行,求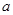 的值;
的值;(Ⅱ)记
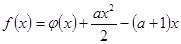 ,
, ,且
,且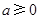 .求函数
.求函数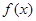 的单调递增区间.
的单调递增区间.(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当 时,函数
时,函数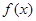 的递增区间是
的递增区间是 ;当
;当 时,函数
时,函数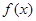 的递增区间是
的递增区间是 ,
, ;当
;当 时,函数
时,函数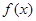 的递增区间是
的递增区间是 ;当
;当 时,函数
时,函数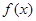 的递增区间是
的递增区间是 ,
, .
.
 ;(Ⅱ)当
;(Ⅱ)当 时,函数
时,函数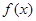 的递增区间是
的递增区间是 ;当
;当 时,函数
时,函数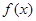 的递增区间是
的递增区间是 ,
, ;当
;当 时,函数
时,函数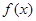 的递增区间是
的递增区间是 ;当
;当 时,函数
时,函数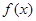 的递增区间是
的递增区间是 ,
, .
.试题分析:(Ⅰ)先求导,由导数的几何意义可得在点
 的导数即为在此点处切线的斜率。从而可得
的导数即为在此点处切线的斜率。从而可得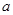 的值。(Ⅱ)先求导整理可得
的值。(Ⅱ)先求导整理可得 ,当
,当 时,
时, ,解导数大于0可得增区间;当
,解导数大于0可得增区间;当 时,导数等于0的两根为
时,导数等于0的两根为 或
或 ,注意对两根大小的讨论,同样解导数大于0可得增区间。
,注意对两根大小的讨论,同样解导数大于0可得增区间。试题解析:(Ⅰ)
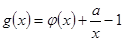 =
= (
( ),
), (
( ),
),因为曲线
 在点
在点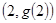 处的切线与直线
处的切线与直线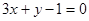 平行,
平行, ,解得
,解得 .
.(Ⅱ)因为

(1)当
 时,
时, .令
.令 解得
解得
(2)
 时
时令
 ,解得
,解得 或
或 .
.(ⅰ)当
 即
即 时,
时,由
 ,及
,及 得
得  .
.解得
 ,或
,或 ;
;(ⅱ)当
 即
即 时,
时,因为
 ,
, 恒成立.
恒成立. (ⅲ)当
 即
即 时,由
时,由 ,及
,及 得
得  .
.解得
 ,或
,或 .
.综上所述,
当
 时,函数
时,函数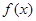 的递增区间是
的递增区间是 ;
;当
 时,函数
时,函数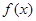 的递增区间是
的递增区间是 ,
, ;
;当
 时,函数
时,函数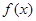 的递增区间是
的递增区间是 ;
;当
 时,函数
时,函数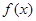 的递增区间是
的递增区间是 ,
, .
.
练习册系列答案
相关题目
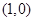 的直线与曲线
的直线与曲线 和
和 都相切,求
都相切,求 的值
的值 (1)求
(1)求 的单调递增区间. (2)已知函数
的单调递增区间. (2)已知函数 )处,切线斜率为
)处,切线斜率为 ,求:
,求: 
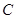 :
: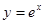 在点
在点 处的切线
处的切线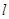 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线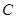 直线
直线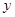 轴围成的图形面积为( )
轴围成的图形面积为( )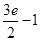
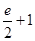
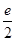
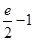
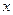 小时,原油温度(单位:℃)为
小时,原油温度(单位:℃)为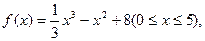 ,那么原油温度的瞬时变化率的最小值为( )
,那么原油温度的瞬时变化率的最小值为( )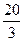
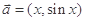 ,
,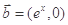 ,若
,若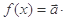
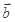 ,则
,则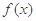 在
在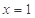 处的切线方程为为.
处的切线方程为为. =1,则(a-c)2+(b-d)2的最小值为________.
=1,则(a-c)2+(b-d)2的最小值为________.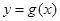 在点
在点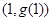 处的切线方程为
处的切线方程为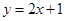 ,则曲线
,则曲线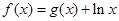 在点
在点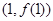 处切线的方程为 .
处切线的方程为 .