题目内容
18.函数f(x)由如表定义:| x | 2 | 5 | 3 | 1 | 4 |
| f(x) | 1 | 2 | 3 | 4 | 5 |
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
分析 由表格可知:f(5)=2,f(2)=1,f(1)=4,f(4)=5,f(3)=3.由于a0=4,an+1=f(an),n=0,1,2,…,可得an+4=an,即可得出.
解答 解:由表格可知:f(5)=2,f(2)=1,f(1)=4,f(4)=5,f(3)=3.
又a0=4,an+1=f(an),n=0,1,2,…,
∴a1=f(a0)=f(4)=5,a2=f(a1)=f(5)=2,a3=f(a2)=f(2)=1,
a4=f(a3)=f(1)=4,a5=f(a4)=f(4)=5,….
∴an+4=an,
∴a2017=a504×4+1=a1=5.
故选D.
点评 本题考查了函数的性质、数列的周期性,考查了归纳法,属于中档题.

练习册系列答案
相关题目
9.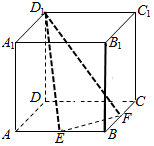 如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )
如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )
 如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )
如图,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,过点D1、E、F的截面将正方体分割成两个部分,记这两个部分的体积分别为V1、V2(V1<V2),则V1:V2=( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{25}{47}$ | D. | $\frac{7}{9}$ |
6.已知i是虚数单位,若$z({1-\frac{1}{2}i})=\frac{1}{2}i$,则|Z|=( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
13.如图,已知四边形ABCD为矩形,PA⊥平面ABCD,下列结论中不一定正确的是( )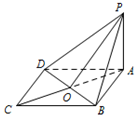

| A. | PD⊥CD | B. | BD⊥平面PAO | C. | PB⊥CB | D. | BC∥平面PAD |
10.已知x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y-2≤0\end{array}\right.$,则z=$\frac{y+1}{x+1}$的范围是( )
| A. | $[\frac{1}{3},2]$ | B. | $[-\frac{1}{2},\frac{1}{2}]$ | C. | $[\frac{1}{2},\frac{3}{2}]$ | D. | $[\frac{3}{2},\frac{5}{2}]$ |