题目内容
8.定义在R上的偶函数y=f(x)满足f(x+1)=-f(x),且当x∈(0,1]时单调递增,则( )| A. | $f(\frac{1}{3})<f(-5)<f(\frac{5}{2})$ | B. | $f(\frac{1}{3})<f(\frac{5}{2})<f(-5)$ | C. | $f(\frac{5}{2})<f(\frac{1}{3})<f(-5)$ | D. | $f(-5)<f(\frac{1}{3})<f(\frac{5}{2})$ |
分析 由f(x+1)=-f(x),得f(x+2)=f(x),即函数为周期函数,利用函数的奇偶性和单调性之间的关系即可得到结论.
解答 解:∵f(x+1)=-f(x),得f(x+2)=f(x),
∴函数是周期为2的周期函数,
则f($\frac{5}{2}$)=f(2+$\frac{1}{2}$)=f($\frac{1}{2}$),
∵函数f(x)是偶函数,∴f(-5)=f(5)=f(1),
∵当x∈(0,1]时单调递增,
∴f($\frac{1}{3}$)<f($\frac{1}{2}$)<f(1),
即$f(\frac{1}{3})<f(\frac{5}{2})<f(-5)$,
故选:B
点评 本题主要考查函数值的大小比较,根据函数的周期性和奇偶性以及单调性之间的关系是解决本题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
17.在△ABC中,a,b,c分别是角A、B、C的对边,且sin2(${\frac{π-A}{2}}$)=$\frac{b+c}{2c}$,则△ABC的形状是( )
| A. | 直角三角形 | B. | 等腰三角形或直角三角形 | ||
| C. | 正三角形 | D. | 等腰直角三角形 |
 某个几何体的三视图如图所示,则该几何体的表面积为$16+4\sqrt{13}$.
某个几何体的三视图如图所示,则该几何体的表面积为$16+4\sqrt{13}$.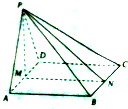 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.