题目内容
18.设a,b,c∈R+,求证:a2ab2bc2c≥ab+cba+cca+b.分析 设a,b,c∈R+,且a≥b≥c,将原不等式作商,整理可得($\frac{a}{b}$)a-b•($\frac{b}{c}$)b-c•($\frac{a}{c}$)a-c.再由指数函数的单调性和不等式的性质即可得证.
解答 证明:设a,b,c∈R+,且a≥b≥c,
$\frac{{a}^{2a}{b}^{2b}{c}^{2c}}{{a}^{b+c}{b}^{a+c}{c}^{a+b}}$=($\frac{a}{b}$)a•($\frac{b}{a}$)b•($\frac{b}{c}$)b•($\frac{c}{b}$)c•($\frac{a}{c}$)a•($\frac{c}{a}$)c
=($\frac{a}{b}$)a-b•($\frac{b}{c}$)b-c•($\frac{a}{c}$)a-c.
由a≥b≥c>0,
可得a-b≥0,b-c≥0,a-c≥0,
$\frac{a}{b}$≥1,$\frac{b}{c}$≥1,$\frac{a}{c}$≥1,
即有($\frac{a}{b}$)a-b≥1,($\frac{b}{c}$)b-c≥1,($\frac{a}{c}$)a-c≥1,
则有($\frac{a}{b}$)a-b•($\frac{b}{c}$)b-c•($\frac{a}{c}$)a-c≥1(当且仅当a=b=c取得等号),
则不等式a2ab2bc2c≥ab+cba+cca+b成立.
点评 本题考查不等式的证明,主要考查作商法证明不等式,同时考查指数函数的单调性的运用,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.已知F是抛物线C:y2=8x的焦点,直线l是抛物线C的准线,点A是l与x轴的交点,点P在抛物线C上,且点P到l的距离为5,则cos∠APF=( )
| A. | $\frac{5}{7}$ | B. | $\frac{2\sqrt{6}}{7}$ | C. | $\frac{29}{35}$ | D. | -$\frac{8\sqrt{6}}{35}$ |
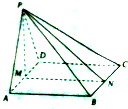 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.