题目内容
已知四面体的三组对棱分别相等,且长分别为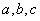 ,则此四面体的外接球的表面积为 .
,则此四面体的外接球的表面积为 .

[解析]由已知中四面体三组对棱棱长分别相等,且其长分别为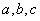 ,故可将其补充为一个长方体,根据外接球的直径等于长方体的对角线,即可求出球的半径.
,故可将其补充为一个长方体,根据外接球的直径等于长方体的对角线,即可求出球的半径.
[说明]让学生熟悉(正)四面体、正(长)方体与球的相接问题.复习时建议探究:
(1)直接利用正四面体来考虑外接球的半径与正四面体高的比值关系并拓展至球与正三棱锥的内切、外接关系.
(2)巩固运算技能,可将必修2(第4版)P69第5题作为当堂训练.

练习册系列答案
相关题目
观察分析下表中的数据:猜想一般凸多面体中F,V,E所满足的等 式是________.
式是________.
| 多面体 | 面数(F) | 顶点数(V) | 棱数(E) |
| 三棱柱 | 5 | 6 | 9 |
| 五棱锥 | 6 | 6 | 10 |
| 立方体 | 6 | 8 | 12 |
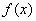 在区间
在区间 上是单调增函数,若
上是单调增函数,若 ,求
,求 的取值范围.
的取值范围. 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上,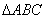 是边长为
是边长为 的正三角形,
的正三角形,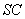 为球
为球 ;则此棱锥的体积为 .
;则此棱锥的体积为 . 中,侧棱垂直底面,
中,侧棱垂直底面, ,
, ,
,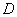 是棱
是棱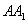 的中点
的中点 平面
平面 ;
; 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
 中,圆C的方程为
中,圆C的方程为 .若直线
.若直线 上存在点
上存在点 ,使过
,使过 的取值范围是 .
的取值范围是 . 中
中 ,前
,前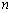 项和为
项和为 ,
,
 ,则
,则 的值为___ __.
的值为___ __.