题目内容
为提高学生的素质,学校决定开设一批选修课程,分别为“文学”、“艺术”、“竞赛”三类,这三类课程所含科目的个数分别占总数的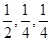 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求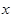 的分布列及期望。
的分布列及期望。
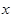 的分布列为
的分布列为
0 1 2 3 p 1/64 9/64 27/64 27/64  9/4
9/4
解析试题分析:设 为3人中选择的科目属于艺术的人数,则
为3人中选择的科目属于艺术的人数,则 ,由题设知
,由题设知 ,
,
则 ,
,
所以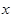 的分布列为
的分布列为
所以
0 1 2 3 p 1/64 9/64 27/64 27/64 
考点:本小题主要考查离散型随机变量的分布列和数学期望.
点评:本题考查离散型随机变量的分布列和数学期望,解题时要认真审题,仔细解答,注意二项分布的性质的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4 人均选科目乙的概率;
(2)设
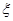 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求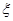 的分布列和数学期望.
的分布列和数学期望. 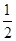 、
、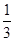 、
、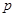 ,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为 .
.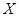 ,求
,求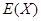 .
. ,不堵车的概率为
,不堵车的概率为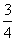 ;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.
;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.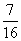 ,求走二号公路堵车的概率;
,求走二号公路堵车的概率;
 表示抽到“极幸福”的人数, 求
表示抽到“极幸福”的人数, 求 ,出现绿灯的概率都是
,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为
.记这4盏灯中出现红灯的数量为 ,当这排装饰灯闪烁一次时:
,当这排装饰灯闪烁一次时: 时的概率;(2)求
时的概率;(2)求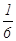 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为 ,两轮检测是否合格相互没有影响。
,两轮检测是否合格相互没有影响。