题目内容
甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为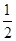
、
、
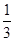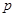，且他们是否破译出密码互不影响，若三人中只有甲破译出密码的概率为
．
（1）求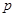的值．
（2）设甲、乙、丙三人中破译出密码的人数为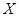
，求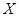的分布列和数学期望
．
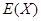（1）
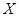
（2）0 1 2 3 P 
解析试题分析：(1)记事件
=”只有甲破译出密码”
,可解得 3分
(2) 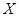的可能取值为0、1,、2、3；
分
8分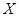0 1 2 3 P 
10分
考点：独立事件的概率
点评：主要是考查了独立事件的概率的公式以及分布列的求解，属于基础题。
练习册系列答案
相关题目
考察某种药物预防甲型H1N1流感的效果，进行动物试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本.
（Ⅰ）根据所给样本数据完成下面2×2列联表；
（Ⅱ）请问能有多大把握认为药物有效？
| | 不得流感 | 得流感 | 总计 |
| 服药 | | | |
| 不服药 | | | |
| 总计 | | | |
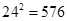） 有甲、乙两个班，进行数学考试，按学生考试及格与不及格统计成绩后，得到如下的列联表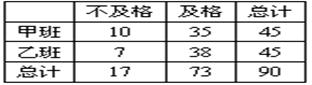
根据表中数据，你有多大把握认为成绩及格与班级有关？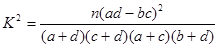
附表：
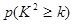 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
的”闯关”游戏. 
则闯关成功. 
，求随机变量某商店试销某种商品，获得如下数据：
| 日销售量（件） | 0 | 1 | 2 | 3 |
| 概率 | 0.05 | 0.25 | 0.45 | 0.25 |
（Ⅰ）求当天商品不进货的概率；
（Ⅱ）记X为第二天开始营业时该商品的件数，求X的分布列和数学期望。
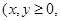且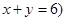
，乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外，无其它区别). 若甲箱从中任取2个球， 从乙箱中任取1个球.
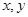的值；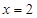
时，求取出的3个球中红球个数
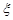的期望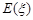
.
，且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力．
，现有3名学生从中任选一个科目参加学习（互不影响），记
为3人中选择的科目属于“文学”或“竞赛”的人数，求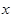
的分布列及期望。