题目内容
由于某高中建设了新校区,为了交通方便要用三辆通勤车从老校区把教师接到新校区.已知从新校区到老校区有两条公路,汽车走一号公路堵车的概率为 ,不堵车的概率为
,不堵车的概率为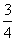 ;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.
;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.
(Ⅰ)若三辆汽车中恰有一辆汽车被堵的概率为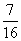 ,求走二号公路堵车的概率;
,求走二号公路堵车的概率;
(Ⅱ)在(Ⅰ)的条件下,求三辆汽车中被堵车辆的个数ξ的分布列和数学期望.
(1)
(2)分布列为
所以E(ξ)=0×ξ 0 1 2 3 P 
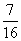


 +1×
+1×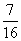 +2×
+2× +3×
+3× =
=
解析试题分析:解:(Ⅰ) 由已知条件得C ·
· ·
·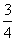 ·(1-p)+(
·(1-p)+(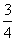 )2·p=
)2·p=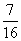 , 3分
, 3分
即3p=1,则p= ,
,
即走二号公路堵车的概率为 . 5分
. 5分
(Ⅱ) ξ可能的取值为0,1,2,3,P(ξ=0)=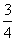 ×
×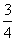 ×
× =
= ,
,
P(ξ=1)=C ×
× ×
×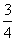 ×
× +
+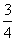 ×
×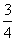 ×
× =
=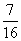 ,
,
P(ξ=2)= ×
× ×
× +C×
+C× ×
×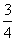 ×
× =
= ,
,
P(ξ=3)= ×
× ×
×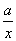 =
= .
.
ξ的分布列为
10分ξ 0 1 2 3 P 
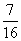


所以E(ξ)=0× +1×
+1×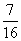 +2×
+2× +3×
+3× =
= . 13分
. 13分
考点:独立重复试验的概率和分布列
点评:主要是考查了分布列和独立重复试验的概率的运用,属于中档题。

 考前必练系列答案
考前必练系列答案有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表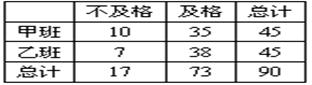
根据表中数据,你有多大把握认为成绩及格与班级有关?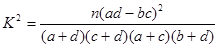
附表:
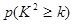 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在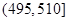 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.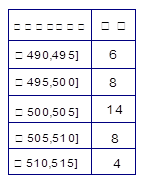
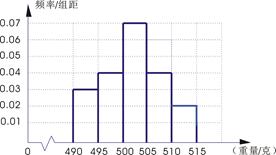
表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面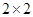 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 | 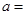 | 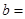 | |
| 不合格品 | 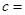 | 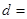 | |
| 合 计 | | |  |
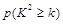 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
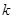 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
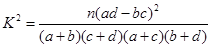 ,其中
,其中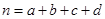 )
)
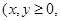 且
且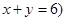 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.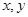 的值;
的值;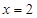 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数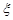 的期望
的期望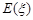 .
.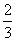 ,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
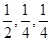 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求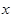 的分布列及期望。
的分布列及期望。 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。 ,求
,求