题目内容
【题目】已知椭圆C的左右顶点分别为A(﹣2,0),B(2,0),椭圆上除A、B外的任一点C满足kACkBC=﹣ ![]() .
. 
(1)求椭圆C的标准方程;
(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N,在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明现由.
【答案】
(1)解:由题意可设椭圆的标准方程为: ![]() =1(a>b>0),
=1(a>b>0),
设椭圆上的任意一点C(x,y),∵kACkBC=﹣ ![]() ,
,
∴ ![]() =﹣
=﹣ ![]() ,整理化为:
,整理化为: ![]() =1.
=1.
点A(﹣2,0),B(2,0),也满足上述方程,
∴椭圆C的标准方程为: ![]() =1
=1
(2)解:假设在x轴上存在点Q,使得∠PQM+∠PQN=180°,
设直线QM,QN的斜率存在,分别设为k1,k2,等价于k1+k2=0.
设直线l的方程为y=k(x﹣4),联立 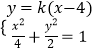 ,化为:(2k2+1)x2﹣16k2x+32k2﹣4=0,
,化为:(2k2+1)x2﹣16k2x+32k2﹣4=0,
则△=256k4﹣4(2k2+1)(32k2﹣4)>0,化为k2 ![]() .
.
设M(x1,y1),N(x2,y2),则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
设Q(m,0),则k1+k2= ![]() +
+ ![]() =0.又y1=k(x1﹣4),y2=k(x2﹣4),
=0.又y1=k(x1﹣4),y2=k(x2﹣4),
化为:k(x1﹣4)(x2﹣m)+k(x2﹣4)(x1﹣m)=0,
∴k=0,或2x1x2﹣(m+4)(x1+x2)+8m=0,
∴2× ![]() ﹣(m+4)×
﹣(m+4)× ![]() +8m=0,化为:m﹣1=0,解得m=1.
+8m=0,化为:m﹣1=0,解得m=1.
k=0时也成立.
综上可得:在x轴上存在点Q(1,0),使得∠PQM+∠PQN=180°
【解析】(1)由题意可设椭圆的标准方程为: ![]() =1(a>b>0),设椭圆上的任意一点C(x,y),由kACkBC=﹣
=1(a>b>0),设椭圆上的任意一点C(x,y),由kACkBC=﹣ ![]() ,利用斜率计算公式可得
,利用斜率计算公式可得 ![]() =﹣
=﹣ ![]() ,整理化简即可得出.(2)假设在x轴上存在点Q,使得∠PQM+∠PQN=180°,设直线QM,QN的斜率存在,分别设为k1 , k2 , 等价于k1+k2=0.设直线l的方程为y=k(x﹣4),与椭圆方程联立化为:(2k2+1)x2﹣16k2x+32k2﹣4=0,设M(x1 , y1),N(x2 , y2),设Q(m,0),则k1+k2=
,整理化简即可得出.(2)假设在x轴上存在点Q,使得∠PQM+∠PQN=180°,设直线QM,QN的斜率存在,分别设为k1 , k2 , 等价于k1+k2=0.设直线l的方程为y=k(x﹣4),与椭圆方程联立化为:(2k2+1)x2﹣16k2x+32k2﹣4=0,设M(x1 , y1),N(x2 , y2),设Q(m,0),则k1+k2= ![]() +
+ ![]() =0.化为:k(x1﹣4)(x2﹣m)+k(x2﹣4)(x1﹣m)=0,把根与系数的关系代入即可得出.
=0.化为:k(x1﹣4)(x2﹣m)+k(x2﹣4)(x1﹣m)=0,把根与系数的关系代入即可得出.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.