题目内容
(本小题满分16分)在数列 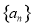 中,已知
中,已知 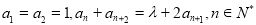 ,
,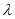 为常数.
为常数.
(1)证明: 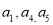 成等差数列;
成等差数列;
(2)设 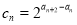 ,求数列 的前n项和
,求数列 的前n项和 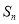 ;
;
(3)当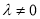 时,数列
时,数列 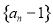 中是否存在三项
中是否存在三项 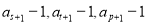 成等比数列,且
成等比数列,且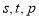 也成等比数列?若存在,求出
也成等比数列?若存在,求出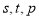 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1)详见解析,
(2)当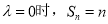 ,当
,当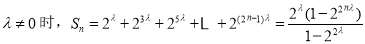
(3)不存在
【解析】
试题分析:(1)判定三项成等差数列,基本方法为验证:分别求出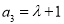 ,
,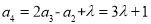 ,
,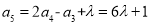 ,满足
,满足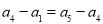 (2)将条件
(2)将条件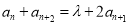 变形为
变形为 ,从而
,从而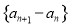 是以0为首项,公差为
是以0为首项,公差为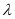 的等差数列,即
的等差数列,即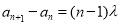 ,所以
,所以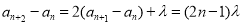 ,
,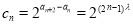 ,当
,当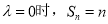 ,当
,当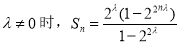 (3)由(2)用累加法可求得
(3)由(2)用累加法可求得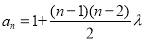 ,假设存在三项
,假设存在三项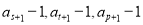 成等比数列,且
成等比数列,且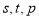 也成等比数列,则
也成等比数列,则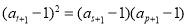 ,即
,即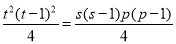 ,
,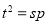 ,化简得
,化简得 ,得
,得 .矛盾.
.矛盾.
试题解析:(1)因为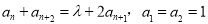 ,
,
所以 ,
,
同理,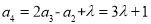 ,
,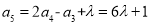 , 2分
, 2分
又因为 ,
,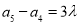 , 3分
, 3分
所以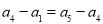 ,
,
故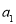 ,
, ,
,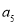 成等差数列. 4分
成等差数列. 4分
(2)由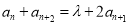 ,得
,得 , 5分
, 5分
令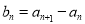 ,则
,则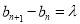 ,
,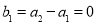 ,
,
所以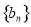 是以0为首项,公差为
是以0为首项,公差为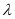 的等差数列,
的等差数列,
所以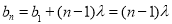 , 6分
, 6分
即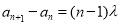 ,
,
所以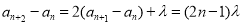 ,
,
所以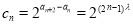 . 8分
. 8分
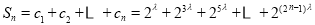
当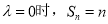 , 9分
, 9分
当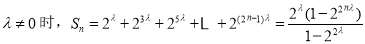 . 10分
. 10分
(3)由(2)知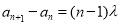 ,
,
用累加法可求得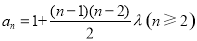 ,
,
当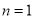 时也适合,所以
时也适合,所以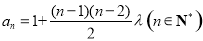 12分
12分
假设存在三项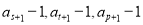 成等比数列,且
成等比数列,且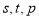 也成等比数列,
也成等比数列,
则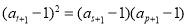 ,即
,即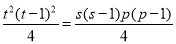 , 14分
, 14分
因为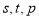 成等比数列,所以
成等比数列,所以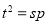 ,
,
所以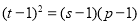 ,
,
化简得 ,联立
,联立 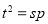 ,得
,得 .
.
这与题设矛盾.
故不存在三项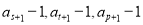 成等比数列,且
成等比数列,且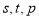 也成等比数列. 16分
也成等比数列. 16分
考点:叠加法数列通项

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
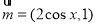 ,
,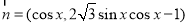 ,函数
,函数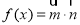 .
.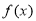 的单调递增区间;
的单调递增区间;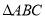 中,角
中,角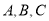 的对边分别为
的对边分别为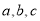 ,若
,若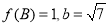 ,
, ,求
,求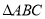
 有两个极值点
有两个极值点 ,
, ,且
,且 ,则( )
,则( ) B.
B.
 D.
D.
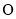 为原点,双曲线
为原点,双曲线 (
(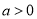 )上有一点
)上有一点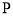 ,过
,过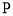 作两条渐近线的平行线,且与两渐近线的交点分别为
作两条渐近线的平行线,且与两渐近线的交点分别为 ,
,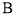 ,平行四边形
,平行四边形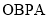 的面积为
的面积为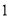 ,则双曲线的离心率为( )
,则双曲线的离心率为( )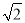 B.
B.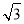 C.
C.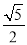 D.
D.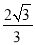
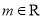 ,则“
,则“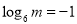 ”是“直线
”是“直线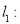
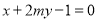 与
与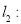
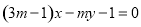 平行”的( )
平行”的( ) ,点D满足
,点D满足 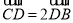 ,且
,且 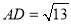 ,则BC的长为_______ .
,则BC的长为_______ .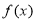 是定义在R上的奇函数,当
是定义在R上的奇函数,当 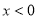 时
时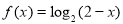 ,则
,则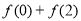 的值为_____.
的值为_____. 平面ABC.
平面ABC.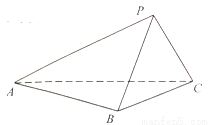
 BC,CP
BC,CP PB,求证:CP
PB,求证:CP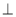 PA:
PA: ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC.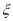 ,求
,求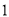 个新球的概率.
个新球的概率. 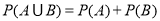 (事件
(事件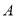 与事件
与事件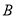 互斥).
互斥).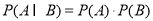 (事件
(事件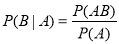 .
.