题目内容
3.在平面直角坐标系xOy中,点P为椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的下顶点,M,N在椭圆上,若四边形OPMN为平行四边形,α为直线ON的倾斜角,若α∈($\frac{π}{6}$,$\frac{π}{4}$],则椭圆C的离心率的取值范围为( )| A. | (0,$\frac{\sqrt{6}}{3}$] | B. | (0,$\frac{\sqrt{3}}{2}$] | C. | [$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{3}}{2}$] | D. | [$\frac{\sqrt{6}}{3}$,$\frac{2\sqrt{2}}{3}$] |
分析 由已知设M(x,-$\frac{a}{2}$),N(x,$\frac{a}{2}$),?代入椭圆方程,得N($\frac{\sqrt{3}}{2}$b,$\frac{a}{2}$),由α为直线ON的倾斜角,得cotα=$\frac{\sqrt{3}b}{a}$,由此能求出椭圆C的离心率的取值范围.
解答 解:∵OP在y轴上,且平行四边形中,MN∥OP,
∴M、N两点的横坐标相等,
纵坐标互为相反数,即M,N两点关于x轴对称,MN=OP=a,
可设M(x,-$\frac{a}{2}$),N(x,$\frac{a}{2}$),?
代入椭圆方程得:|x|=$\frac{\sqrt{3}}{2}$b,得N($\frac{\sqrt{3}}{2}$b,$\frac{a}{2}$),
α为直线ON的倾斜角,tanα=$\frac{\frac{a}{2}}{\frac{\sqrt{3}}{2}b}$=$\frac{a}{\sqrt{3}b}$,cotα=$\frac{\sqrt{3}b}{a}$,
α∈($\frac{π}{6}$,$\frac{π}{4}$],∴1≤cotα=$\frac{\sqrt{3}b}{a}$≤$\sqrt{3}$,
$\frac{\sqrt{3}}{3}≤\frac{b}{a}≤1$,∴$\frac{1}{3}≤\frac{{b}^{2}}{{a}^{2}}≤1$,
∴0<e=$\sqrt{1-\frac{{a}^{2}}{{b}^{2}}}$≤$\frac{\sqrt{6}}{3}$.
∴椭圆C的离心率的取值范围为(0,$\frac{\sqrt{6}}{3}$].
故选:A.
点评 本题旨在考查解析几何椭圆的离心率问题.考查数形结合和运算能力,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

| A. | ∅ | B. | (0,3) | C. | (-5,4) | D. | (0,4) |
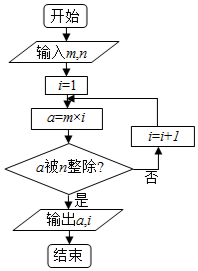 当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )
当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )| A. | 37${C}_{12}^{7}$ | B. | 38${C}_{12}^{8}$ | C. | -33${C}_{12}^{3}$ | D. | -37${C}_{12}^{5}$ |
| A. | y=2x-1+1(x>2) | B. | y=2x+1+1(x>0) | C. | y=2x-1-1(x>2) | D. | y=2x+1-1(x>0) |