题目内容
已知函数f(x)=
,若对于任意x∈[1-2a,1+2a],不等式f(x+a)≤f(2x)恒成立,则实数a的取值范围是 .
|
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:易知函数f(x)在定义域内是增函数,所以要使f(x+a)≤f(2x)恒成立,只需x+a≤2x恒成立在x∈[1-2a,1+2a]时,只需a≤x的最小值即可,然后结合区间有意义,可将问题解决.
解答:
解:首先1-2a<1+2a,所以a>0.
易知函数函数f(x)=
在R上单调递增,
所以要使对于任意x∈[1-2a,1+2a],不等式f(x+a)≤f(2x)恒成立,
只需x+a≤2x,即a≤x,当x∈[1-2a,1+2a]时恒成立.
只需a≤xmin=1-2a即可.
解得a≤
.
综上可知0<a≤
即为所求.
故答案为(0,
].
易知函数函数f(x)=
|
所以要使对于任意x∈[1-2a,1+2a],不等式f(x+a)≤f(2x)恒成立,
只需x+a≤2x,即a≤x,当x∈[1-2a,1+2a]时恒成立.
只需a≤xmin=1-2a即可.
解得a≤
| 1 |
| 3 |
综上可知0<a≤
| 1 |
| 3 |
故答案为(0,
| 1 |
| 3 |
点评:本题考查了不等式恒成立问题的解题思路,一般转化为函数的最值问题来解,要注意对函数单调性的分析.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
在数38,47,56,65中,最大的一个是( )
| A、38 |
| B、47 |
| C、56 |
| D、65 |
已知函数f(x)是定义在[-1,1]上的奇函数,对于任意x1,x2∈[-1,1],x1≠x2,总有
>0且f(1)=1.若对于任意α∈[-1,1],使f(x)≤t2-2αt-1成立,则实数t的取值范围是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、-2≤t≤2 | ||||
B、t≤-1-
| ||||
| C、t≤0或t≥2 | ||||
| D、t≥2或t≤-2或t=0 |
已知全集U={x|0<x<9},A={x|1<x<a},若非空集合A⊆U,则实数a的取值范围是( )
| A、(-∞,9) |
| B、(-∞,9] |
| C、(1,9) |
| D、(1,9] |
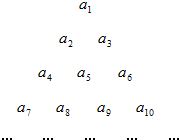 已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=
已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n= 如图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是
如图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是