题目内容
如图是一个几何体的三视图（侧视图中的弧线是半圆），则该几何体的表面积是考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由几何体的三视图，知该几何体的上半部分是棱长为2的正方体，下半部分是半径为1，高为2的圆柱的一半，由此能求出该几何体的表面积．
解答：
解：由几何体的三视图，知该几何体的上半部分是棱长为2的正方体，下半部分是半径为1，高为2的圆柱的一半，
∴该几何体的表面积S=5×22+π×12+
×2π×1×2=20+3π．
故答案为：20+3π．
∴该几何体的表面积S=5×22+π×12+
| 1 |
| 2 |
故答案为：20+3π．
点评：本题考查由几何体的三视图求几何体的表面积的求法，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
初中学业考试导与练系列答案
相关题目
如图所示的程序框图，若输出的S=41，则判断框内应填入的条件是（ ）
| A、k＞3？ | B、k＞4？ |
| C、k＞5？ | D、k＞6？ |
集合A={x∈N|x≤6}，B={x∈R|x2-3x＞0}，则A∩B=（ ）
| A、{x|3≤x＜6} |
| B、{3，4，5} |
| C、{x|3＜x≤6} |
| D、{4，5，6} |
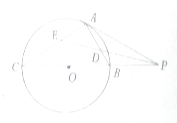如图PA与圆O相切于点A，经过点O的割线PBC交圆O于点B、C，∠APC的平分线分别交AB、AC于点D、E．某几何体的三视图如图所示，则该几何体的表面积是（ ）
| A、90 | B、92 | C、98 | D、104 |
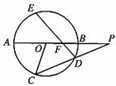如图，⊙O的直径AB=4，弦CD所在直线与AB的延长线交于点P，且