题目内容
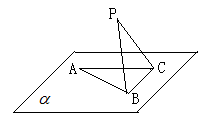
如图,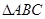 在平面
在平面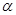 内,
内,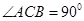 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面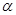 外一个动点,且PC=
外一个动点,且PC=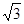 ,
,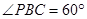
(1)问当PA的长为多少时,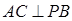
(2)当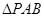 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
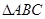 在平面
在平面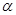 内,
内,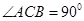 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面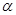 外一个动点,且PC=
外一个动点,且PC=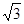 ,
,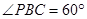

(1)问当PA的长为多少时,
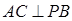
(2)当
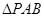 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值(1)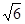 ;(2)
;(2)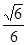
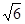 ;(2)
;(2)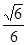
试题分析:(1)由分析可知当
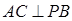 时,
时,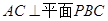 ,则
,则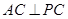 ,由勾股定理可求得
,由勾股定理可求得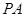 。(2)因为
。(2)因为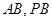 为定值,且
为定值,且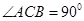 ,
,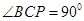 ,所以当
,所以当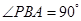 时,
时,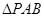 的面积取得最大值。分析可知
的面积取得最大值。分析可知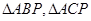 均是以
均是以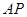 为底的等腰三角形,故取
为底的等腰三角形,故取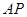 中点
中点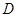 ,连接
,连接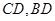 。则有
。则有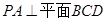 ,从而可得
,从而可得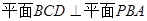 。过
。过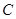 作
作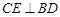 ,E为垂足,从而可得
,E为垂足,从而可得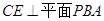 ,所以
,所以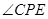 就是直线
就是直线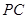 与平面
与平面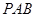 所成角,在
所成角,在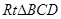 中即可求此角。
中即可求此角。试题解析:(1)因为
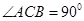 ,所以
,所以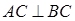 ,当
,当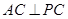 时,
时,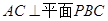 ,而
,而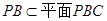 ,所以
,所以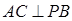 时,此时,
时,此时,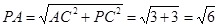 ,即当
,即当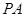 =
=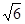 时,
时,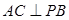
(2)
在
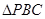 中,因为PC=
中,因为PC=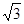 ,
,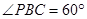 ,
,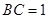 ,所以
,所以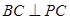 ,
,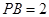 .当
.当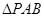 的面积取得最大值时,
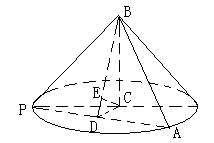
的面积取得最大值时,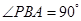 ,(如图)在
,(如图)在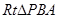 中,因为
中,因为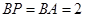 ,取
,取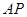 中点
中点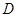 ,连接
,连接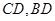 。因为
。因为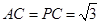 且点
且点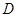 为
为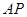 中点,所以
中点,所以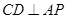 ,因为
,因为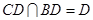 ,所以
,所以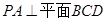 ,由此可求得
,由此可求得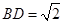 ,又在
,又在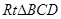 中,
中,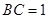 ,所以
,所以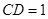 ,过
,过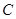 作
作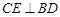 ,E为垂足,由于
,E为垂足,由于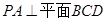 ,所以,
,所以,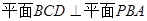 ,由两个平面互相垂直的性质可知:
,由两个平面互相垂直的性质可知: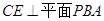 ,所以
,所以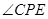 就是直线
就是直线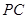 与平面
与平面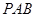 所成角,在
所成角,在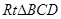 中,可求得
中,可求得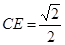 ,在
,在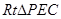 中,
中,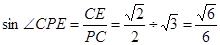 ,所以直线
,所以直线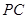 与平面
与平面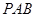 所成角的正弦值是
所成角的正弦值是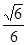 .
.
练习册系列答案
相关题目
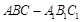 中,侧面
中,侧面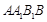 为菱形,且
为菱形,且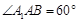 ,
,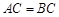 ,
,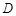 是
是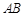 的中点.
的中点.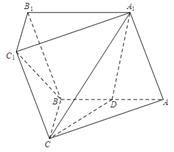
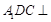 平面
平面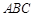 ;
;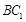 ∥平面
∥平面 .
.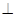 底面ABCD,侧棱
底面ABCD,侧棱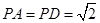 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB
 分别是正方体
分别是正方体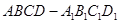 的棱
的棱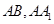 的中点,点
的中点,点 分别是线段
分别是线段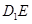 与
与 上的点,则满足与平面
上的点,则满足与平面 平行的直线
平行的直线 有( )
有( )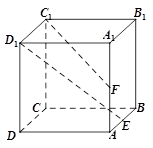
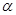 、
、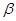 是两个不同的平面,则
是两个不同的平面,则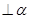 ,则n
,则n
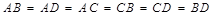 ,则
,则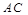 与
与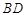 所成角为( )
所成角为( )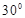
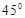
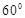
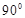
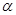 内的两条不同直线,l是平面
内的两条不同直线,l是平面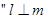 且
且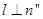 是
是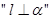 的( )
的( )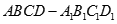 中,下列几种说法错误的是
中,下列几种说法错误的是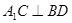
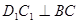
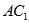 与
与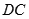 成
成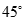 角
角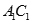 与
与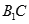 成
成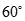 角
角