题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据题意转化为![]() 的最小值小于等于9,二次函数根据轴与区间的关系进行分类讨论,得到答案.(2)利用导数求出
的最小值小于等于9,二次函数根据轴与区间的关系进行分类讨论,得到答案.(2)利用导数求出![]() 的极小值
的极小值![]() 和极大值
和极大值![]() ,并且得到
,并且得到![]()
![]() 的关系,以及
的关系,以及![]() 与
与![]()
![]() 的关系,表示出
的关系,表示出![]() 消去
消去![]() ,然后令
,然后令![]() ,将
,将![]() 转化成关于
转化成关于![]() 的函数,注意
的函数,注意![]() 的取值范围,从而求出
的取值范围,从而求出![]() 的范围.
的范围.
(1)因为![]() ,
,
所以函数![]() 的最小值小于等于9.
的最小值小于等于9.
(i)函数![]() 的对称轴为
的对称轴为![]() ,当
,当![]() ,即
,即![]() 时,
时,
由![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ;
;
(ii)当![]() ,即
,即![]() 时,
时,
由![]() ,得
,得![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.
(2)因为![]() ,所以
,所以![]() .
.
设![]() ,因为
,因为![]() ,
,
所以函数![]() 有两个不同的零点,不妨设为
有两个不同的零点,不妨设为![]() ,
,![]() ,且
,且![]() ,
,
则![]() ,
,![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 为单调递减函数;
为单调递减函数;
当![]() 时,
时,![]() ,函数
,函数![]() 为单调递增函数;
为单调递增函数;
当![]() 时,
时,![]() ,函数
,函数![]() 为单调递减函数.
为单调递减函数.
所以当![]() 时,函数
时,函数![]() 取得极小值,当
取得极小值,当![]() 时,函数
时,函数![]() 取得极大值,
取得极大值,
所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
设![]() ,则
,则![]()
![]() ,
,
所以![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上为单调减函数,
上为单调减函数,
从而![]() ,
,
又![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,
,
即![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.

 长江作业本同步练习册系列答案
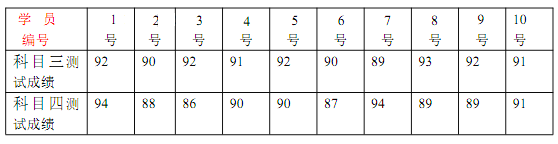
长江作业本同步练习册系列答案【题目】影响消费水平的原因很多,其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法,在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平(单位:万元).
地区 | 上海 | 江苏 | 浙江 | 安徽 | 福建 |
职工平均工资 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城镇居民消费水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平,求出线性回归方程![]() ,其中
,其中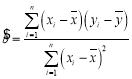
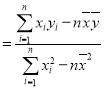 ,
,![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万,则认为得到的线性回归方程是可靠的,试问所得的线性回归方程是否可靠?(![]() 的结果保留两位小数)
的结果保留两位小数)
(参考数据:![]() ,
,![]() )
)
【题目】微信运动是由腾讯开发的一个类似计步数据库的公众账号,很多手机用户加入微信运动后,为了让自己的步数能领先于朋友,运动的积极性明显增强.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
|
|
|
|
|
|
|
|
| 5 | 20 | 50 | 18 | 3 | 3 | 1 |
(Ⅰ)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;
(Ⅱ)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;
(Ⅲ)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有![]() 人,超过1.2万步的有
人,超过1.2万步的有![]() 人,设
人,设![]() ,求的分布列及数学期望.
,求的分布列及数学期望.

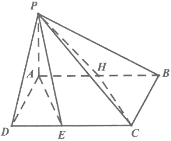
【题目】
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分,不低于85分称优秀)人数之间的关系进行分析研究,他们从本校初二,初三,高一,高二,高三年级各随机抽取了40名学生,记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数,得到如下数据表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工(单位:小时) | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y(单位:人) | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,再用剩下的2组数据进行检验.
(1)若选取的是初三,高一,高二的3组数据,请根据这3组数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?
参考数据:![]() ,
,![]() .
.
参考公式: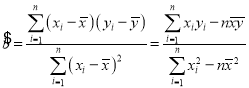 ,
,![]() .
.