��Ŀ����
7�� ��ͼ��������ABCD�ı߳�Ϊ2��OΪAD���е㣬����OP��OA���������ŵ�O˳ʱ�뷽����ת��OD������ת�Ĺ����У��ǡ�AOPΪx��x��[0���У���OP����������������ABCD�ڵ�������Ӱ���֣������S=f��x������ô���ں���f��x���������������ۣ�������ȷ���ǣ�������
��ͼ��������ABCD�ı߳�Ϊ2��OΪAD���е㣬����OP��OA���������ŵ�O˳ʱ�뷽����ת��OD������ת�Ĺ����У��ǡ�AOPΪx��x��[0���У���OP����������������ABCD�ڵ�������Ӱ���֣������S=f��x������ô���ں���f��x���������������ۣ�������ȷ���ǣ���������f��$\frac{��}{3}$��=$\frac{\sqrt{3}}{2}$
�ں���f��x���ڣ�$\frac{��}{2}$���У���Ϊ������
������x��[0��$\frac{��}{2}$]������f��x��+f����-x��=4��
| A�� | �� | B�� | �� | C�� | �٢� | D�� | �٢� |
���� ��ͼ�οɵú����Ľ���ʽ���ٷֱ��жϣ����ɵó����ۣ�
��� �⣺��0��x��arctan2ʱ��f��x��=$\frac{1}{2}$tanx��
��arctan2��x��$\frac{��}{2}$���ڡ�OBE�У�f��x��=S����OABM-S��OME
=2-$\frac{1}{2}$EM•OM=2-$\frac{2}{tanx}$��
��x=$\frac{��}{2}$ʱ��f��x��=2��
��$\frac{��}{2}$��x�ܦ�-arctan2ʱ��ͬ���ɵ�f��x��=2-$\frac{2}{tanx}$��
����-arctan2��x�ܦ�ʱ��f��x��=4-$\frac{1}{2}$��1��tan����-x��=4+$\frac{1}{2}$tanx�����ǿɵã�
��f��$\frac{��}{3}$��=$\frac{1}{2}$tan$\frac{��}{3}$=$\frac{\sqrt{3}}{2}$����ȷ��
�ڵ�$\frac{��}{2}$��x�ܦ�-arctan2ʱ����f��x��=2-$\frac{2}{tanx}$��Ϊ������������-arctan2��x�ܦ�ʱ��f��x��=4+$\frac{1}{2}$tanx��Ϊ����������˲���ȷ��
��?x��[0��$\frac{��}{2}$]����ͼ�μ������棬���öԳ��Կɵã�f��x��+f����-x��=4�������ȷ��
��ѡC��
���� ���⿼����ͼ������ļ��㡢���к����ĵ����ԡ����������ж��������˷�������˼�뷽����������������������������е��⣮

| A�� | $��{3\sqrt{2}��\frac{3��}{4}}��$ | B�� | $��{3\sqrt{2}��\frac{5��}{4}}��$ | C�� | $��{3��\frac{5��}{4}}��$ | D�� | $��{3��\frac{3��}{4}}��$ |
| A�� | {-2��-1��0��1��2} | B�� | {-1��2��3} | C�� | {-2��-1��0��1��2��3} | D�� | {-1��2} |
| A�� | 143 | B�� | 144 | C�� | 287 | D�� | 288 |
| A�� | [-3��3] | B�� | [-1��2] | C�� | [-3��2] | D�� | ��-1��2] |




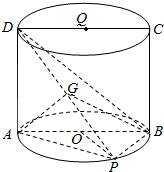 ��ͼ���ı���ABCD�����Ϊ8$\sqrt{3}$�е�Բ��OQ������棬��P�ڵ���Բ���ϣ�BP=OA=2��G��DP���е㣮
��ͼ���ı���ABCD�����Ϊ8$\sqrt{3}$�е�Բ��OQ������棬��P�ڵ���Բ���ϣ�BP=OA=2��G��DP���е㣮