题目内容
已知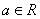 ,函数
,函数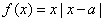 .
.
(1)当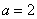 时,写出函数
时,写出函数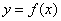 的单调递增区间;
的单调递增区间;
(2)当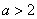 时,求函数
时,求函数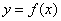 在区间
在区间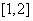 上的最小值;
上的最小值;
(3)设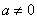 ,函数
,函数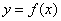 在
在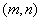 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出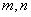 的取值范围(用
的取值范围(用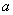 表示).
表示).
(1)当 时,
时, ,
,
由图象可知, 的单调递增区间为
的单调递增区间为 .
.
(2)因为 ,所以
,所以 .
.
当 ,即
,即 时,
时, ;
;
当 ,即
,即 时,
时, .
. .
.
(3) ,
,
①当 时,图象如图1所示.
时,图象如图1所示.
由 得
得 .
.


图1 图2
②当 时,图象如图2所示.
时,图象如图2所示.
由 得
得 .
.

练习册系列答案
相关题目
 ,9本不同的语文书,8本不同的英语书,从中任取两本不同类的书,共有________种不同的取法.
,9本不同的语文书,8本不同的英语书,从中任取两本不同类的书,共有________种不同的取法. 的三角形
的三角形 的面积的最大值为 .
的面积的最大值为 . ,则满足
,则满足 时
时 的取值范围是 .
的取值范围是 .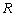 上的偶函数
上的偶函数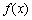 满足:
满足: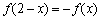 ,且在
,且在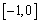 上是增函数,下面关于
上是增函数,下面关于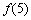 =0;③
=0;③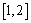 上是减函数;④
上是减函数;④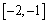 上是减函数,其中正确的判断是 .(把你认为正确的判断都填上)
上是减函数,其中正确的判断是 .(把你认为正确的判断都填上) ”的否定是________.
”的否定是________. 对应的点在第________象限.
对应的点在第________象限.
 分别交x轴正半轴及y轴负半轴于M、N两点,点P为圆C上任意一点,则
分别交x轴正半轴及y轴负半轴于M、N两点,点P为圆C上任意一点,则 的最大值为__________.
的最大值为__________.