题目内容
7.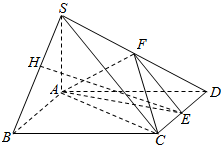 如图所示,已知四棱锥S-ABCD,底面ABCD为菱形,∠ABC=60°,SA⊥平面ABCD,E,F分别是CD,SD的中点,点H为SB上的动点,且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$.
如图所示,已知四棱锥S-ABCD,底面ABCD为菱形,∠ABC=60°,SA⊥平面ABCD,E,F分别是CD,SD的中点,点H为SB上的动点,且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$.(1)证明:AE⊥SB;
(2)求二面角E-AF-C的余弦值.
分析 (1)根据线面垂直的性质定理即可证明:AE⊥SB;
(2)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角E-AF-C的余弦值
解答 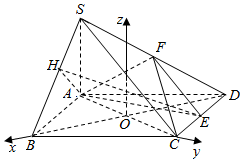 (1)证明:∵底面ABCD为菱形,∠ABC=60°,
(1)证明:∵底面ABCD为菱形,∠ABC=60°,
∴△ACD是正三角形,
∵E是CD的中点,∴AE⊥CD,
即AE⊥AB,
∵SA⊥平面ABCD,AE?平面ABCD,
∴SA⊥AE,
∵AB∩SA=A,
∴AE⊥平面SAB,
∵SB?平面SAB,
∴AE⊥SB;
(2)由(1)知AE⊥平面SAB,
则AH是EH在平面SAB的射影,
即AH⊥SB,
∠AHE是EH与平面SAB所成最大角,
即tan∠AHE=$\frac{\sqrt{6}}{2}$.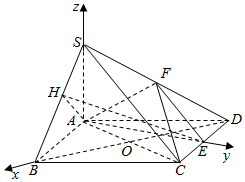
设菱形的边长为2,即AB=2,AC=2,
则AE=$\sqrt{3}$,
由tan∠AHE=$\frac{AE}{AH}$=$\frac{\sqrt{3}}{AH}$=$\frac{\sqrt{6}}{2}$.
则AH=$\sqrt{2}$,
∵AB=2,
∴sin∠ABH=$\frac{AH}{AB}=\frac{\sqrt{2}}{2}$,则∠ABH=45°,
则△SAB是等腰三角形,则SA=AB=2,
建立以A为坐标原点,AB,AE,AS分别为x,y,z轴,建立空间直角坐标系如图:
则A(0,0,0),E(0,$\sqrt{3}$,0),C(1,$\sqrt{3}$,0),D(-1,$\sqrt{3}$,0),S(0,0,2),F(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,1),
设平面EAF的法向量为$\overrightarrow{m}$=(x,y,z),
平面CAF的法向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{AF}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,1),
$\overrightarrow{AE}$=(0,$\sqrt{3}$,0),$\overrightarrow{AC}$=(1,$\sqrt{3}$,0),
则由$\overrightarrow{m}$•$\overrightarrow{AF}$=-$\frac{1}{2}$x+$\frac{\sqrt{3}}{2}$y+z=0,$\overrightarrow{m}$•$\overrightarrow{AE}$=$\sqrt{3}$y=0,
得y=0,令x=2,则z=1,即$\overrightarrow{m}$=(2,0,1),
由$\overrightarrow{n}$•$\overrightarrow{AF}$=-$\frac{1}{2}$x+$\frac{\sqrt{3}}{2}$y+z=0,$\overrightarrow{n}$•$\overrightarrow{AC}$=x+$\sqrt{3}$y=0,
令y=-$\sqrt{3}$,则x=3,z=3,即$\overrightarrow{n}$=(3,-$\sqrt{3}$,3),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2×3+1×3}{\sqrt{{2}^{2}+1}•\sqrt{{3}^{2}+(-\sqrt{3})^{2}+{3}^{2}}}$=$\frac{9}{\sqrt{5}•\sqrt{21}}$=$\frac{3\sqrt{105}}{35}$,
即二面角E-AF-C的余弦值是=$\frac{3\sqrt{105}}{35}$.
点评 本题主要考查直线垂直的判定,以及二面角的求解,建立坐标系,利用向量法进行求解,综合性较强,运算量较大.

| A. | (-2,2] | B. | (-2,1] | C. | (0,3) | D. | (1,3) |
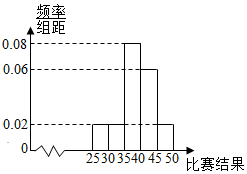 为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:
为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:| 年龄所在区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
(1)求人数统计表中的a和b的值;
(2)根据频率分布直方图,估计该项比赛结果的中位数;
(3)用分层抽样的方法从第1,2,3组中共抽取6人,再从这6人中随机抽取2人参加上一级比赛活动,求参加上一级比赛活动中至少有1人的比赛结果在第3组的概率.

| A. |  | B. |  | C. |  | D. |  |
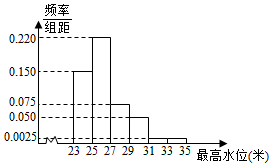 根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:
根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图: