题目内容
3.过椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的一个焦点作垂直于长轴的弦,则此弦长为( )| A. | $\frac{3}{4}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | $\frac{{8\sqrt{3}}}{3}$ |
分析 利用椭圆的标准方程即可得出c,进而得出弦AB的坐标及弦长.
解答 解:椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1,可得a2=4,b2=3,∴c=$\sqrt{{a}^{2}-{b}^{2}}$=1.
不妨取焦点F(1,0),过焦点F作垂直于长轴的椭圆的弦为AB,$\frac{1}{4}$+$\frac{{y}^{2}}{3}$=1,解得y=±$\frac{3}{2}$.
∴弦长|AB|=2×$\frac{3}{2}$=3.
故选:C.
点评 熟练掌握椭圆的标准方程及其性质是解题的关键.

练习册系列答案
相关题目
11.一个球从100米高处自由落下,每次着地后又跳回至前一次高度的一半落下,当它第10次着地时,共经过的路程为 (结果精确到1米)( )
| A. | 199米 | B. | 200米 | C. | 300米 | D. | 100米 |
18.已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到抛物线准线的距离为( )
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
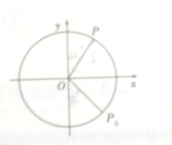 如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0($\sqrt{2}$,-$\sqrt{2}$),角速度为1,点P到x轴的距离d是关于时间t的函数,当t=$\frac{π}{4}$时,d=0.
如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0($\sqrt{2}$,-$\sqrt{2}$),角速度为1,点P到x轴的距离d是关于时间t的函数,当t=$\frac{π}{4}$时,d=0. 已知函数f(x)=x|x-2|,
已知函数f(x)=x|x-2|,