题目内容
【题目】设椭圆E的方程为 
+y2=1（a＞1），O为坐标原点，直线l与椭圆E交于点A，B，M为线段AB的中点．
（1）若A，B分别为E的左顶点和上顶点，且OM的斜率为﹣ 
，求E的标准方程；
（2）若a=2，且|OM|=1，求△AOB面积的最大值．
【答案】
（1）解：设M（x0，y0），A（x1，y1），B（x2，y2），
则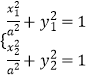 
，两式相减，得 
，
即 
，又 
，
代入化简，解得a=2，
故E的标准方程为 
（2）解：设直线l：x=my+n，A（x1，y1），B（x2，y2），
∴ 
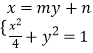，整理得：（4+m2）y2+3mny+n2﹣4=0①
y1+y2=﹣ 
，y1y2= 
，x1+x2= 
，
由中点坐标公式可知：M（ 
， 
），即M（ 
，﹣ 
）
∵|OM|=1，
∴n2= 
②，
设直线l与x轴的交点为D（n，0），
则 
，
令 
，
设t=m2+4（t≥4），
则 
，
当t=12时，即 
时，
△AOB的面积取得最大值1
【解析】（1）将A和B代入椭圆方程，做差求得 ，由斜率公式可知kAB= ，即可求得a的值，求得E的标准方程；（2）将直线方程代入椭圆方程，由韦达定理及中点坐标公式，即可求得M点坐标，由|OM|=1，可得n2= ，由三角形面积公式可知： ，t=m2+4（t≥4），代入由基本不等式的性质即可求得△AOB面积的最大值．
练习册系列答案
相关题目
